- Kirjoittaja Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Viimeksi muokattu 2025-01-23 12:17.
Siirtyminen fysiikassa tarkoittaa objektin sijainnin muutosta. Kun lasket siirtymää, lasket kuinka kauas kohde sijaitsee sen alkuperäisen ja lopullisen sijainnin perusteella. Kaava, jota käytät siirtymän laskemiseen, riippuu ongelmaan annetusta muuttujasta. Laske siirtymä seuraavasti.
Vaihe
Osa 1/5: Tuloksen siirtymän laskeminen

Vaihe 1. Käytä tuloksena olevaa siirtymäkaavaa, jos etäisyysyksikköä käytetään osoittamaan aloitus- ja lopetuspaikat
Vaikka etäisyys eroaa siirtymästä, tuloksena oleva siirtymäongelma etsii kuinka monta kilometriä tai metriä kohde on kulkenut. Tämän mittayksikön avulla voit laskea siirtymän ja sen, kuinka kaukana kohteen sijainti poikkeaa sen lähtöpisteestä.
- Tuloksena oleva siirtymäkaava kirjoitetaan seuraavasti: S = x²+y². S on siirtymä. X on kohteen ensimmäinen liikesuunta ja Y on kohteen toinen liikesuunta. Jos kohde liikkuu vain yhteen suuntaan, niin Y = 0.
- Objekti voi liikkua enintään kahteen suuntaan, koska liikkumista pohjois-/etelä- tai itä/länsi -akselia pitkin pidetään neutraalina liikkeenä.

Vaihe 2. Yhdistä pisteet liikejärjestyksessä ja merkitse ne kohdasta A-Z
Piirrä viivaimella suora viiva pisteestä pisteeseen.
- Muista myös yhdistää lähtöpisteesi päätepisteeseesi suoralla viivalla. Tämä on siirtymä, jonka laskemme.
- Jos kohde esimerkiksi liikkuu itään 300 m ja pohjoiseen 400 m, se muodostaa suorakulmion. AB on kolmion ensimmäinen jalka ja BC on toinen jalka. AC on kolmion hypotenuusa ja sen suuruus on kohteen siirtymä. Tässä esimerkissä kaksi suuntaa ovat itä ja pohjoinen.

Vaihe 3. Anna arvot x² ja y²
Nyt kun tiedät objektisi kaksi liikesuuntaa, syötä arvot sopiviin muuttujiin.
Esimerkiksi x = 300 ja y = 400. Kaavan pitäisi näyttää tältä: S = 300² + 400²
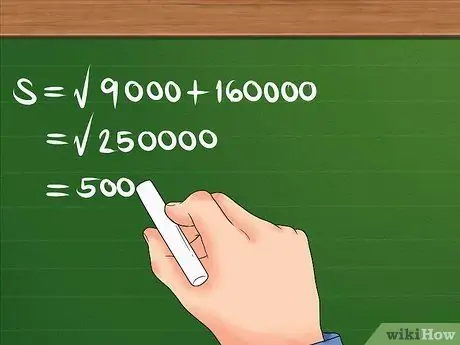
Vaihe 4. Laske kaava toimintojen järjestyksen mukaan
Neliöt 300 ja 400, laske ne yhteen ja etsi summan neliöjuuri.
Esimerkiksi: S = 90000 + 160000. S = 250000. S = 500. Nyt tiedät, että siirtymä on 500 m
Osa 2/5: Kun nopeus ja aika tiedetään

Vaihe 1. Käytä tätä kaavaa, kun ongelma kertoo objektin nopeuden ja sen keston
Jotkut matemaattiset ongelmat eivät kerro sinulle, kuinka pitkälle tai kuinka nopeasti esine liikkuu. Voit laskea siirtymän käyttämällä tätä ajan suuruutta ja nopeutta.
-
Tässä tapauksessa kaava on seuraava: S = 1/2 (u + v) t.
U = kohteen alkunopeus tai kuinka nopeasti kohde alkaa liikkua tiettyyn suuntaan. V = kohteen lopullinen nopeus tai kuinka nopeasti esine liikkuu kohti lopullista sijaintiaan. T = aika, joka kuluu kohteesta lopullisen sijaintinsa saavuttamiseen.
- Esimerkki: Auto ajaa tiellä 45 sekuntia (vaadittu aika). Auto kääntyy länteen nopeudella 20 m/s (alkunopeus) ja tien lopussa sen nopeus on 23 m/s (lopullinen nopeus). Laske siirtymä näiden tekijöiden perusteella.

Vaihe 2. Syötä haluttu nopeus ja aika sopiviin muuttujiin
Nyt kun tiedät kuinka pitkälle auto liikkuu, kuinka nopeasti auto liikkuu alussa ja lopussa, voit löytää etäisyyden lähtöpaikasta lopulliseen sijaintiin.
Kaavasi pitäisi näyttää tältä: S = 1/2 (20 + 23) 45

Vaihe 3. Laske kaava sen jälkeen, kun olet asettanut arvot oikeaan paikkaan
Muista noudattaa toimintojen järjestystä, muuten siirtymät johtavat hyvin erilaisiin arvoihin.
- Tällä kaavalla ei ole väliä, jos vaihdat vahingossa aloitus- ja lopetusnopeutta. Koska lisäät nämä numerot ensin yhteen, ei ole väliä, missä ne ovat suluissa. Muiden kaavojen osalta alkunopeuden ja lopullisen nopeuden vaihtaminen johtaa erilaisiin siirtymäarvoihin.
- Kaavan pitäisi näyttää tältä: S = 1/2 (43) 45. Jaa ensin 43 kahdella, jolloin tuloksena on 21, 5. Kerro sitten 21, 5 45: llä, jolloin tulos on 967,5 metriä. 967, 5 on siirtymän suuruus tai kuinka pitkälle auto on siirtynyt lähtöpisteestään.
Osa 3/5: Kun alkunopeus, kiihtyvyys ja aika tiedetään
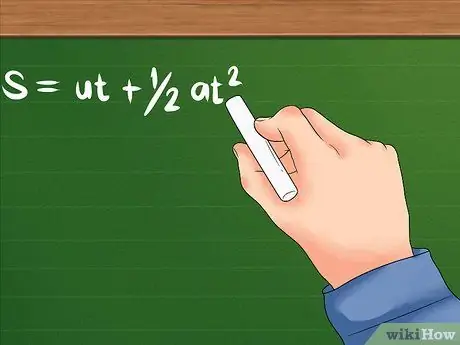
Vaihe 1. Käytä muokattua kaavaa, kun kiihtyvyys tiedetään alkuperäisen nopeuden ja ajan lisäksi
Jotkut kysymykset kertovat vain, kuinka nopeasti esine liikkuu alussa, kuinka nopeasti kohde alkaa kiihtyä ja kuinka pitkälle kohde liikkuu. Tarvitset seuraavan kaavan.
- Tämän ongelman kaava on seuraava: S = ut + 1/2 at². U osoittaa edelleen alkunopeutta; a on kohteen kiihtyvyys tai kuinka nopeasti sen nopeus alkaa muuttua. T voi tarkoittaa aikaa, joka kestää tai tietyn ajan, joka kestää kohteen kiihtymisen. Molemmat käyttävät aikayksiköitä, kuten sekunteja, tunteja ja muita.
- Oletetaan, että auto, joka liikkuu nopeudella 25 m/s (alkunopeus), alkaa kiihtyä nopeudella 3 m/s2 (kiihtyvyys) 4 sekunnin ajan (aika). Mikä on auton siirtymä 4 sekunnin kuluttua?

Vaihe 2. Anna arvot kaavaan
Toisin kuin edellinen kaava, tässä esitetään vain alkunopeus, joten muista syöttää oikeat tiedot.
Yllä olevien esimerkkitietojen perusteella kaava näyttäisi tältä: S = 25 (4) + 1/2 (3) 4². Se auttaa lisäämään sulkuja kiihtyvyyden suuruuden ja ajan ympärille, jotta voit erottaa numerot
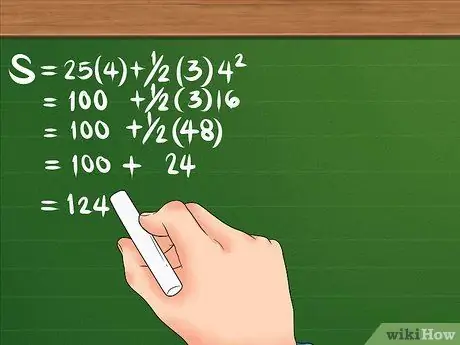
Vaihe 3. Laske siirtymä tekemällä se oikeassa toimintojärjestyksessä
Nopea tapa auttaa sinua muistamaan toimintojen järjestys on aasin silta Kur ir Kua ci Kadang Ba wa Juragan Turtles. Tämä edustaa oikeaa järjestystä: sulkeet, neliöt, kertolasku, jako, summaus ja vähennys.
Katsotaanpa kaavaa uudelleen: S = 25 (4) + 1/2 (3) 4². Ensinnäkin neliö 4, tulos on 16. Kerro sitten 16 kolmella, jolloin saat 48; kerro sitten myös 25 x 4, jolloin saat 100. Jaa 48 kahdella, niin saat 24. Sinun yhtälön pitäisi näyttää tältä: S = 100 + 24. Kun lisäät nämä kaksi yhteen, siirtymä on 124 metriä
Osa 4/5: Kulman siirtymän laskeminen

Vaihe 1. Etsi kulmasiirtymä, kun kohde liikkuu ympyräradalla
Vaikka lasket edelleen siirtymää käyttämällä suoraa viivaa, sinun on löydettävä ero kohteen alkamis- ja päättymispaikkojen välillä sen liikkuessa pyöreällä reitillä.
- Kuvittele tyttö istuvan karusellilla. Pyöriessään karusellilla hän liikkuu pyöreällä polulla. Kulmasiirtymä yrittää löytää lyhyimmän etäisyyden alkuperäisen ja lopullisen sijainnin välillä, kun kohde ei liiku suorassa linjassa.
- Kulman siirtymän kaava on: = S/r, jossa S on lineaarinen siirtymä, r on säde ja on kulmapoikkeama. Lineaarinen siirtymä on se, kuinka pitkälle esine liikkuu kaaria pitkin. Säde on kohteen etäisyys ympyrän keskipisteeseen. Kulman siirtymä on arvo, jonka haluamme löytää.

Vaihe 2. Liitä lineaarinen siirtymä ja säde yhtälöön
Muista, että säde on etäisyys ympyrän keskipisteestä; Jotkut ongelmat kertovat ympyrän halkaisijan, joka on jaettava kahdella säteen löytämiseksi.
- Tässä on esimerkki ongelmasta: tyttö ratsastaa karusellilla. Istuin on 1 metrin päässä ympyrän keskipisteestä (säde). Jos tyttö liikkuu valokaarireitillä 1,5 metriä (lineaarinen siirtymä), mikä on hänen kulmasiirtymänsä?
- Yhtälösi näyttää tältä: = 1,5/1.
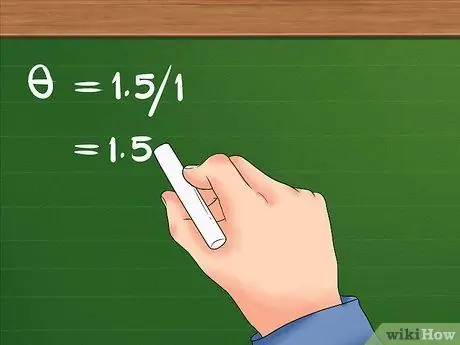
Vaihe 3. Jaa lineaarinen siirtymä säteellä
Tämä jako johtaa kohteen kulmaliikkeeseen.
- Kun 1,5 on jaettu 1: llä, tulos on 1.5. Tytön kulmasiirtymä on 1.5 radiaanit.
- Koska kulmasiirtymä mittaa kuinka paljon esine pyörii alkuperäisestä asennostaan, se on mitattava kulman, ei etäisyyden mukaan. Radiaania käytetään kulmien mittaamiseen.
Osa 5/5: Tietoa muuttoliikkeestä
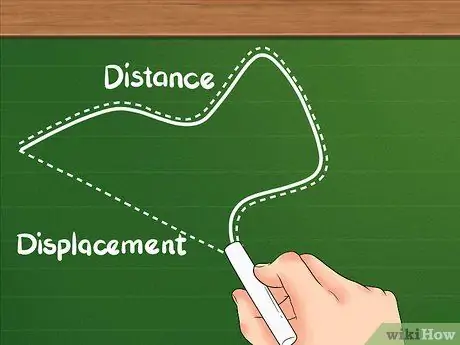
Vaihe 1. Tiedä, että etäisyydellä on erilainen määritelmä kuin siirtymällä
Etäisyys näyttää, kuinka pitkä kohteen kokonaismatka on.
- Etäisyys tunnetaan usein skalaarisena suurena. Etäisyys näyttää kohteen kulkeman matkan kohteen suunnasta riippumatta.
- Jos esimerkiksi kävelet 2 askelta itään, 2 askelta etelään, 2 askelta länteen ja sitten 2 askelta pohjoiseen, palaat lähtöasentoosi. Vaikka olet käynyt läpi kaiken etäisyys 10 askeleen päässä, sinä vain liikkua 0 askeleen päässä, koska lopullinen sijaintisi on sama kuin lähtöpaikka (polkusi muistuttaa laatikkoa).

Vaihe 2. Ymmärrä, että siirtymä on kahden sijainnin välinen ero
Siirtymä ei ole liikkeen kokonaissumma, kuten etäisyys; siirtyy keskittymään aloitus- ja lopetuspaikkojen väliseen alueeseen.
- Siirtymää kutsutaan vektorin suureksi ja se osoittaa objektin sijainnin muutoksen ottaen huomioon kohteen liikesuunnan.
- Esimerkiksi kävelet itään 5 askelta. Jos palaat länteen 5 askelta, siirryt vastakkaiseen suuntaan alkuperäisestä sijainnistasi. Vaikka olet käynyt läpi 10 vaihetta, asemasi ei ole muuttunut; siirtymäsi on 0 askelta.

Vaihe 3. Muista sanat eteenpäin ja taaksepäin, kun yrität kuvitella siirtymistä
Vastakkaiseen suuntaan liikkuminen eliminoi esineen siirtymisen.
Kuvittele jalkapallovalmentaja edestakaisin sivussa. Kun hän huusi pelaajille, hän siirtyi vasemmalta oikealle useita kertoja. Jos katsot häntä, kun hän liikkuu vasemmalta oikealle, näet koko matkan, jonka hän on kulkenut. Oletetaan kuitenkin, että valmentaja pysähtyy puhumaan pelinrakentajan kanssa sivussa. Jos hän on eri paikassa kuin alkuperäinen sijaintinsa ennen muuttoa, tarkkailet kouluttajan liikettä

Vaihe 4. Tiedä, että siirtymä mitataan käyttämällä suoraa polkua, ei pyöreää polkua
Jos haluat löytää siirtymän, sinun on löydettävä lyhin ja tehokkain tapa laskea kahden pisteen välinen ero.
- Pyöreä polku vie sinut lähtöpaikastasi lopulliseen sijaintiisi, mutta se ei ole lyhin polku. Jotta voisit visualisoida sen, kuvittele, että kävelet suorassa linjassa ja törmäät pilariin. Et voi murtaa tätä pylvästä, joten kierrät sen ympäri. Vaikka lopullinen asemasi on sama kuin murtautuisit pilarin läpi, tarvitset lisätoimia tämän tavoitteen saavuttamiseksi.
- Vaikka siirtymä edustaa suoraa polkua, muista, että voit mitata kohteen siirtymän tällä hetkellä liikkua pyöreällä tiellä. Tätä siirtymää kutsutaan kulmasiirtymäksi ja se voidaan laskea etsimällä lyhin polku alkuperäisestä sijainnista lopulliseen sijaintiin.

Vaihe 5. Tiedä, että siirtymä voi olla negatiivinen, toisin kuin etäisyys
Jos lopullinen sijainti saavutetaan siirtymällä vastakkaiseen suuntaan alkuperäiseen suuntaan, siirtymäsi on negatiivinen.
- Esimerkiksi kävelemme 5 askelta itään ja sitten 3 askelta länteen. Vaikka lasket laskemalla 2 askelta lähtöpaikastasi, siirtymäsi on -2, koska liikut vastakkaiseen suuntaan. Etäisyytesi on aina positiivinen, koska et voi laskea taaksepäin askeleissa, kilometreissä jne.
- Negatiivinen siirtymä ei tarkoita, että siirtymä vähenee. Negatiivinen tarkoittaa vain sitä, että suunta on päinvastainen.

Vaihe 6. Huomaa, että joskus etäisyys ja siirtymä voivat olla samat
Jos kävelet suoraan 25 askelta ja pysähdyt, matka kulkee yhtä paljon kuin siirtymä alkuperäisestä sijainnistasi.
- Tämä pätee vain, kun siirryt yhdestä paikasta lähtöpaikastasi suoralla linjalla. Esimerkiksi asut San Franciscossa, Kaliforniassa, ja saat uuden työpaikan Las Vegasissa, Nevadassa. Sinun on muutettava Las Vegasiin ollaksesi lähellä työpaikkaa. Jos nouset lentokoneeseen suoraan San Franciscosta Las Vegasiin matkustat saman matkan ja siirtymän x.
- Jos kuitenkin ajaa San Franciscosta Las Vegasiin, matkustat matkan x, mutta y y. Koska autolla ajamisella on yleensä vaihtelevat suunnat (tämän tien itäpuolella, tien länsipuolella), matkustat pidempiä matkoja kuin lyhin etäisyys kahden kaupungin välillä.






