Matematiikassa prosenttimuutoksen käsitettä käytetään kuvaamaan vanhan arvon ja uuden arvon välistä suhdetta. Tarkemmin sanottuna prosentuaalinen muutos edustaa vanhan ja uuden prosenttiosuuden välistä eroa prosentteina vanhasta arvosta. Käytä kaavaa ((V2 - V1) / V1) × 100eli V.1 edustaa vanhaa tai alkuarvoa ja V2 heijastavat uutta tai nykyistä arvoa. Jos luku on positiivinen, se osoittaa prosentuaalisen nousun ja jos se on negatiivinen, se osoittaa prosenttilaskun. Voit myös käyttää muokattua kaavaa laskeaksesi prosentuaalisen vähenemisen negatiivisen luvun sijasta.
Vaihe
Menetelmä 1/2: Vakiokaavojen käyttö
Vaihe 1. Vähennä uusi arvo alkuperäisestä arvosta
Prosentuaalista lisäystä laskettaessa pienempi luku on alkuperäinen (tai vanha) luku ja suurempi arvo on uusi (tai lopullinen) arvo. Ja päinvastoin, kun haluat laskea prosenttilaskun. Tämän kaavan avulla voit laskea prosentuaalisen lisäyksen tai vähennyksen. Jos vastauksesi on negatiivinen luku positiivisen luvun sijasta, prosenttiosuus on pienentynyt.
- Oletetaan esimerkiksi, että yrität selvittää, kuinka paljon tulosi ovat kasvaneet vuodesta toiseen. Jos teit 37 000 dollaria viime vuonna ja 45 dollaria tänä vuonna, vähennä 45 000 000 37 000 000: sta, mikä tekee 8 000 000.
- Muuten vähittäiskaupassa alennetut tuotteet kirjoitetaan yleensä "alennus x%", mikä on prosenttiosuus. Jos housut myytiin aiemmin hintaan 500 000 IDR ja nyt 300 000 IDR, alkuarvo on 500 000 IDR ja uusi arvo 300 000 IDR. Aloita vähentämällä 300 000 dollaria 500 dollarista, mikä tekee -200 000 dollaria.
Kärki:
Kun lasket muuttujan, jossa on useita arvomuutoksia, etsi prosentuaalinen muutos vain kahdelle vertailukelpoiselle arvolle.
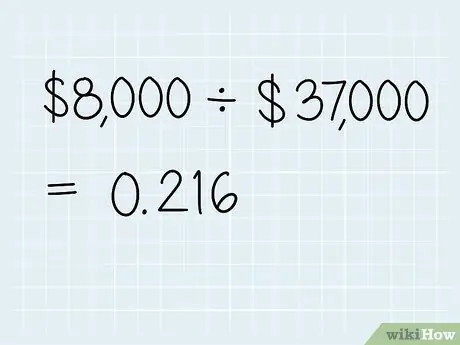
Vaihe 2. Jaa vastaus alkuperäisellä arvolla
Kun olet laskenut arvoeron, jaa tulos alkuperäisellä numerolla, joka on pieni luku, jos prosenttiosuus kasvaa, ja suuri luku, jos prosenttiosuus pienenee.
- Jatka edellistä esimerkkiä jakamalla 8 000 000 (tuloero) 37 000 000: lla (joka on alkuarvo). Vastaus on 0, 216.
- Muussa tapauksessa erotus (-200 000 ruplaa) vanhalla arvolla (500 000 ruplaa) on -0,40. Yksi tapa ajatella sitä on, että 200 000 ruplan arvon muutos on 0,40 500 000 ruplan lähtökohdasta ja muutosarvo negatiiviseen suuntaan.
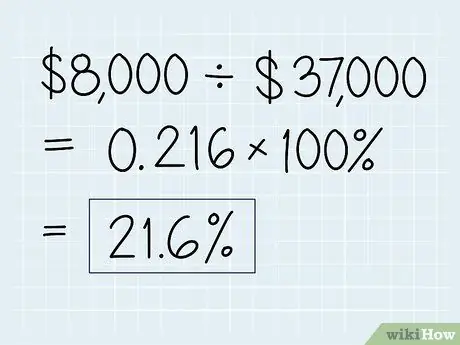
Vaihe 3. Kerro vastaus 100: lla
Jos haluat muuntaa vastauksen prosenttiosuudeksi, sinun on vain kerrottava vastaus 100: lla. Jos haluat muuntaa sen prosentiksi, sinun on vain kerrottava se 100: lla.
- Ota 0,216 ja kerro 100: lla. Tässä tapauksessa vastaus on 21,6, joten tulosi kasvavat 21,6%.
- Muussa tapauksessa lopullisen prosenttiosuuden saamiseksi kerro desimaalivastaus (-0, 40) 100: lla. -0, 40 × 100 = -40%. Tämä tarkoittaa, että uusi 300 000 ruplan hinta on 40% pienempi kuin vanha 500 000 ruplan hinta. Toisin sanoen housut ovat 40% alennuksessa. Toinen tapa ajatella sitä on, että 200 000 dollarin hintaero on 40% 500 000 dollarin alkuperäisestä hinnasta. Koska alkuperäinen hinta on suurempi kuin lopullinen hinta, anna negatiivinen symboli.
Menetelmä 2/2: Prosenttilaskun laskeminen muilla tavoilla
Vaihe 1. Vähennä alkuperäinen arvo uudella arvolla
Jos haluat laskea prosentuaalisen vähenemisen tällä kaavalla, vähennä suurempi arvo (alkuperäinen tai alkuarvo) pienemmällä arvolla (uusi tai lopullinen arvo). Huomaa, että tämä on päinvastoin prosenttiosuuksien löytämisessä käyttämällä vakioyhtälöä.
Oletetaan esimerkiksi, että yrität selvittää, kuinka paljon uusien opiskelijoiden määrä muuttuu vuosittain. Jos uusia oppilaita oli tänä vuonna 12 125 ja viime vuonna 13 500, vähennä 13 125 12 125: sta, jolloin saat 1 375
Vaihe 2. Jaa vastaukset alkuperäisten pisteiden kanssa
Muista, että prosenttiosuuden vähennystä määritettäessä alkuperäinen arvo on suurempi luku.
Jaa tässä tapauksessa 1,375 (kahden arvon välinen ero) 12,125: llä (alkuperäinen arvo), joka palauttaa arvon 0,1143
Vaihe 3. Kerro vastaus 100: lla
Muunna vastaus desimaalista prosenttiin kertomalla se 100: lla.
Kerro 0, 1134 100: lla, mikä on 11, 34. Joten uusien opiskelijoiden määrä väheni 11, 34%
Kärki:
Jos käytät tätä yhtälöä ja saat negatiivisen luvun, tämä tarkoittaa prosentuaalista lisäystä.
