Objektiivin suurennuksen laskeminen: 12 vaihetta (kuvilla)

2024 Kirjoittaja: Jason Gerald | [email protected]. Viimeksi muokattu: 2024-01-16 19:26

Optisia instrumentteja tutkittaessa linssimaisen kohteen "suurennus" on näkemäsi kuvan korkeuden suhde kohteen todelliseen korkeuteen. Esimerkiksi objektiivilla, joka voi saada kohteen näyttämään erittäin suurelta, on "suuri" suurennuskerroin, kun taas objektiivilla, joka saa esineen näyttämään pieneltä, on "pieni" suurennuskerroin. Kohteen suurennuskaava lasketaan yleensä kaavan avulla M = (h_i/h_o) = -(d_i/d_o), jossa M = suurennus, h_i = kuvan korkeus, h_o = kohteen korkeus ja d_i ja D_o = kuvan ja kohteen etäisyys.

Vaihe

Menetelmä 1 /2: Yhden objektiivin suurennuksen laskeminen

Huomautuksia: A lähentyvä linssi leveämpi keskellä kuin reunat (kuten suurennuslasi). a hajottava linssi leveämpi reunoilta kuin keskeltä (kuten kulho). Suurennuksen laskeminen molemmilla objektiiveilla on sama yksi tärkeä poikkeus. Napsauta tästä siirtyäksesi suoraan poikkeaviin objektiiveihin.

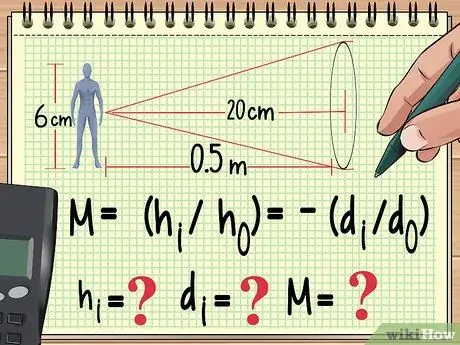
Vaihe 1. Aloita yhtälöstäsi ja jo tiedetyistä muuttujista

Aivan kuten mikä tahansa muu fysiikkaongelma, tapa ratkaista laajentumisongelma on kirjoittaa ylös yhtälö, jota käytät sen laskemiseen. Täältä voit työskennellä taaksepäin löytääksesi muuttujan arvon, jota et ole löytänyt käyttämästäsi yhtälöstä.

Oletetaan esimerkiksi, että 6 cm pitkä nukke on sijoitettu metrin päähän lähentyvä linssi polttovälillä 20 cm. Jos haluamme laskea suurennuksen, kuvan korkeuden ja kuvan etäisyyden, voimme aloittaa yhtälön kirjoittamisen seuraavasti:

M = (h_i/h_o) = -(d_i/d_o)
Nyt tiedämme h_o (nuken korkeus) ja d_o (nuken etäisyys linssistä). Tiedämme myös linssin polttovälin, joka ei ole tässä yhtälössä. Laskemme h_i, d_ija M.

Vaihe 2. Linssiyhtälön käyttäminen d: n saamiseksi_i.

Jos tiedät etäisyyden suurennettavasta kohteesta ja linssin polttovälin, etäisyyden laskeminen muodostetusta kuvasta on erittäin helppoa objektiivin yhtälön avulla. Linssin yhtälö on 1/f = 1/d_o + 1/d_i, jossa f = linssin polttoväli.

Tässä esimerkkitehtävässä voimme käyttää linssiyhtälöä d: n laskemiseen_i. Syötä arvot f ja d_i ratkaise sitten yhtälö:

1/f = 1/d_o + 1/d_i

1/20 = 1/50 + 1/d_i

5/100 - 2/100 = 1/p_i

3/100 = 1/p_i

100/3 = d_i = 33,3 cm
Linssin polttoväli on etäisyys linssin keskipisteestä pisteeseen, jossa valo siirtyy polttopisteeseen. Jos olet koskaan kohdentanut valon suurennuslasilla palaviin muurahaisiin, olet nähnyt sen. Oppitunnin kysymyksissä on yleensä ilmoitettu tämän hotspotin suuruus. Tosielämässä nämä tekniset tiedot on yleensä kirjoitettu objektiivin tarraan.

Vaihe 3. h: n laskeminen_i.

Laskennan jälkeen d_o ja D_i, voit laskea suurennetun kohteen korkeuden ja linssin suurennuksen. Huomaa kaksi yhtäläisyysmerkkiä linssin suurennusyhtälössä (M = (h_i/h_o) = -(d_i/d_o)) - tämä tarkoittaa, että kaikki tämän yhtälön osat ovat keskenään yhtä suuret, joten voimme laskea M ja h_i missä järjestyksessä tahansa haluamme.

Tässä esimerkkitehtävässä voimme laskea h_i kuten tämä:

(h_i/h_o) = -(d_i/d_o)

(h_i/6) = -(33, 3/50)

h_i = -(33, 3/50) x 6

h_i = - 3, 996 cm
Huomaa, että objektin korkeus on negatiivinen, mikä osoittaa, että myöhemmin näkemämme kuva käännetään (ylhäältä alas).

Vaihe 4. M: n laskeminen

Voit laskea viimeisen muuttujan yhtälöllä -(d_i/d_o) tai (h_i/h_o).

Seuraavassa esimerkissä M: n laskeminen on seuraava:

M = (h_i/h_o)

M = (-3, 996/6) = - 0, 666
Tulos on myös sama laskettaessa d: n arvolla:

M = -(d_i/d_o)

M = -(33, 3/50) = - 0, 666
Huomaa, että zoomauksessa ei ole yksikkömerkkiä.

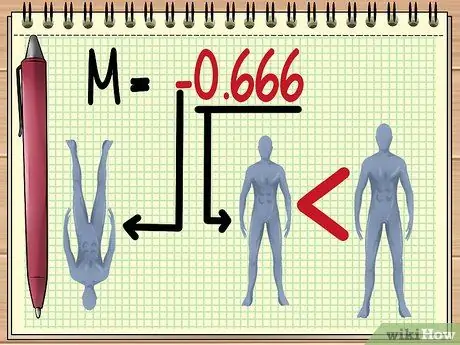
Vaihe 5. M -arvon ymmärtäminen

Kun olet saanut M -arvon suuruuden, voit arvioida useita asioita objektiivin läpi näkyvästä kuvasta, nimittäin:

Koko.

Mitä suurempi M: n "absoluuttinen arvo", sitä suurempi objektiivi näyttää objektiivilta. M -arvo välillä 0 - 1 osoittaa, että kohde näyttää pienemmältä.
Kohteen suunta.

Negatiivinen arvo osoittaa, että muodostettu kuva käännetään.
Tässä annetussa esimerkissä M -arvo -0,666 tarkoittaa, että olemassa olevan muuttujan arvon mukaan nuken varjo tulee näkyviin. ylösalaisin ja kaksi kolmasosaa todellista kokoa pienempi.

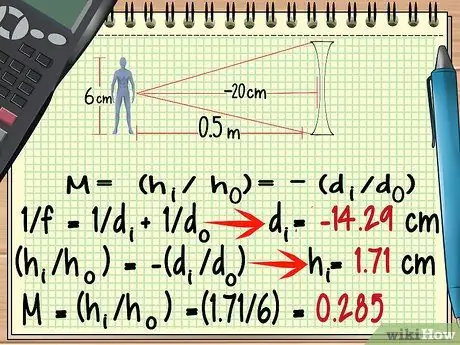
Vaihe 6. Käytä hajautuvan linssin kohdalla negatiivista polttoväliä

Vaikka poikkeavan linssin muoto on hyvin erilainen kuin lähentyvän linssin, voit laskea sen suurennuksen käyttämällä samaa kaavaa kuin yllä. Poikkeukset, jotka on pidettävä mielessä, ovat Eri linssien polttoväli on negatiivinen.

Yllä olevassa esimerkkitehtävässä tämä vaikuttaa vastaukseen, jonka saat laskettaessa d_i, joten muista kiinnittää huomiota tähän.

Katsotaanpa uudelleen yllä olevaa esimerkkiongelmaa, vasta nyt käytämme poikkeavaa objektiivia, jonka polttoväli on - 20 cm.

Muut muuttujat pysyvät samana.
Ensinnäkin laskemme d_i käyttämällä linssin yhtälöä:

1/f = 1/d_o + 1/d_i

1/-20 = 1/50 + 1/d_i

-5/100 - 2/100 = 1/pv_i

-7/100 = 1/pv_i

-100/7 = d_i = - 14, 29 cm
Nyt laskemme h_i ja M, jonka arvo on d_i uusi.

(h_i/h_o) = -(d_i/d_o)

(h_i/6) = -(-14, 29/50)

h_i = -(-14, 29/50) x 6

h_i = 1,71 cm

M = (h_i/h_o)

M = (1, 71/6) = 0, 285

Menetelmä 2/2: Useiden objektiivien suurennuksen laskeminen

Yksinkertainen kahden linssin menetelmä

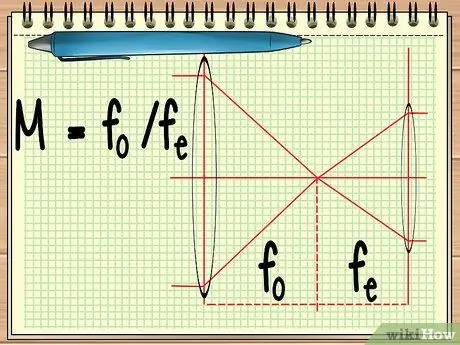
Vaihe 1. Laske kahden linssin polttoväli

Kun käytät instrumenttia, joka koostuu kahdesta vierekkäin asetetusta linssistä (kuten kaukoputki tai kiikari), sinun tarvitsee vain selvittää kahden linssin keskipiste laskeaksesi molempien linssien kokonaissuurennuksen. tämä voidaan laskea yksinkertaisella yhtälöllä M = f_o/f_e.

Yhtälössä f_o on objektiivin keskipiste ja f_e on okulaarin keskipiste. Objektiivilinssi on suuri linssi, joka on lähellä kohdetta, kun taas silmälinssi on linssi, joka sijaitsee lähellä tarkkailijan silmää.

Vaihe 2. Liitä jo olemassa olevat tiedot yhtälöön M = f_o/f_e.

Kun sinulla on molempien linssien polttovälit, niiden laskeminen on erittäin helppoa, - laske suhde jakamalla objektiivin polttoväli okulaarin polttovälillä. Saamasi vastaus on työkalun kokonaissuurennos.

Oletetaan esimerkiksi, että yksinkertainen kaukoputki on kirjoitettu, että objektiivin polttoväli on 10 cm ja okulaarin polttoväli on 5 cm, jolloin suurennos on 10/5 = 2.

Monimutkainen menetelmä

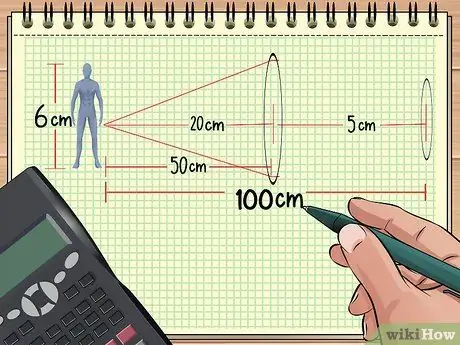
Vaihe 1. Laske etäisyys linssien ja kohteen välillä

Jos sinulla on kaksi objektiivia peräkkäin kohteen edessä, kokonaissuurennus voidaan laskea, jos tiedät etäisyyden linssistä kohteeseen, kohteen koon ja kahden linssin polttovälin. Loput voidaan myös laskea.

Oletetaan esimerkiksi, että järjestämme esineitä ja linssejä yllä olevan esimerkkitehtävän 1 mukaisesti: nukke on 50 cm: n päässä 20 cm: n polttovälestä. Aseta nyt toinen objektiivi, jonka polttoväli on 5 cm, 50 cm: n etäisyydelle ensimmäisestä linssistä (100 cm: n päässä nukesta.) Tämän jälkeen laskemme kokonaissuurennuksen saamiemme tietojen perusteella

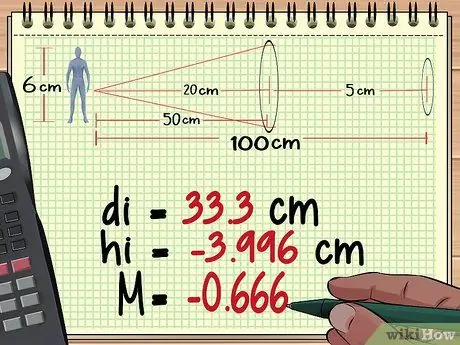
Vaihe 2. Laske objektin etäisyys, korkeus ja suurennos linssistä 1

Useiden linssien suurennuksen laskemisen ensimmäinen osa on sama kuin yksittäisen linssin suurennuksen laskeminen. Aloita objektiivia lähinnä olevasta objektiivista, etsi etäisyys muodostuneesta kuvasta linssin yhtälön avulla ja etsi sitten kuvan korkeus ja suurennus suurennusyhtälön avulla. Napsauta tätä nähdäksesi lisää yhden linssin suurennuslaskelmia.

Yllä olevan menetelmän 1 laskelmiemme perusteella havaitsemme, että ensimmäinen linssi tuottaa jopa korkean kuvan - 3, 996 cm, etäisyys 33,3 cm linssin takana ja suurennuksella - 0, 666.

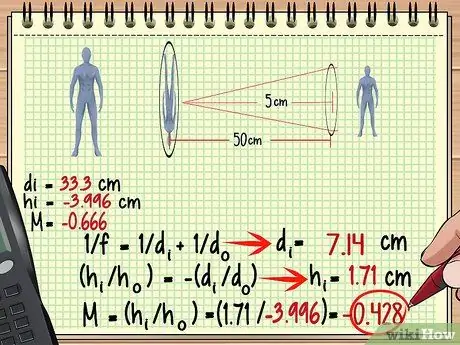
Vaihe 3. Käytä ensimmäisen linssin kuvaa toisen objektiivin kohteena

Nyt toisen objektiivin suurennuksen, korkeuden ja muiden ominaisuuksien löytäminen on erittäin helppoa - käytä samaa menetelmää, jota käytit ensimmäisessä linssissä, tällä kertaa vain kohtele kuvaa. Muista, että kuvan etäisyys toiseen objektiiviin ei aina ole sama kuin kohteen etäisyys ensimmäiseen linssiin.

Yllä olevassa esimerkissä, koska kuva muodostuu 33,3 cm ensimmäisen linssin taakse, etäisyys on 50-33,3 = 16,7 cm toisen linssin edessä. Käytä tätä mittausta ja toisen linssin polttoväliä löytääksesi toisen linssin muodostaman kuvan.

1/f = 1/d_o + 1/p_i

1/5 = 1/16, 7 + 1/d_i

0, 2-0, 0599 = 1/pv_i

0, 14 = 1/p_i

d_i = 7,14 cm
Nyt voimme laskea h_i ja M toiselle linssille:

(h_i/h_o) = -(d_i/d_o)

(h_i/-3, 996) = -(7, 14/16, 7)

h_i = -(0, 427) x -3, 996

h_i = 1,71 cm

M = (h_i/h_o)

M = (1, 71/-3, 996) = - 0, 428

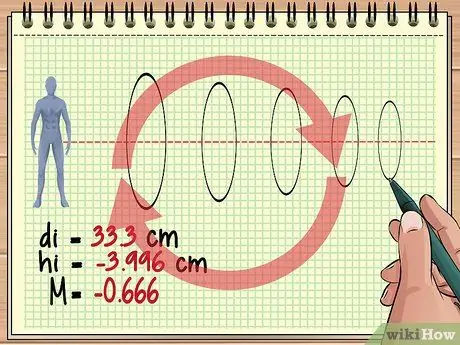
Vaihe 4. Jatka laskemista näin lisälinsseille

Tämä peruslähestymistapa on sama, jos esineen edessä on kolme, neljä tai satoja linssejä. Pidä jokaisen objektiivin kohdalla objektiivina edellisen linssin kuvaa ja löydä haluamasi vastaus linssin yhtälön ja suurennusyhtälön avulla.

Muista, että jokainen seuraava linssi voi jatkuvasti kääntää muodostetun kuvan. Esimerkiksi aikaisemmin saatu suurennusarvo (-0, 428) osoittaa, että näkemämme kuva on noin 4/10 kohteen todellisesta koosta, mutta kohtisuorassa, koska edellisen linssin kuva on käänteinen

Vinkkejä

Kiikarit selittävät yleensä suurennustiedot lukumäärällä toisen numeron muodossa. Esimerkiksi kiikarit voidaan määrittää 8x25 tai 8x40. Kun näin kirjoitetaan, ensimmäinen numero on kiikarin suurennos. Sillä ei ole väliä, vaikka annetussa esimerkissä kaksi numeroa ovat suuruudeltaan erilaisia, molemmilla kiikareilla on 8 -kertainen suurennus. Toinen numero osoittaa, kuinka kirkas kuva muodostaa kiikarit.
Muista, että yhden linssin luupin suurennus on negatiivinen, jos kohteen etäisyys on suurempi kuin linssin polttoväli. Tämä ei tarkoita, että muodostettu kuva olisi pienempi. Tässä tapauksessa suurennus tapahtuu edelleen, mutta tarkkailija näkee muodostuneen kuvan ylösalaisin (ylhäältä alas).