- Kirjoittaja Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Viimeksi muokattu 2025-01-23 12:17.
Jokainen voi oppia matematiikkaa riippumatta siitä, onko hän jo korkeammassa vaiheessa koulussa vai haluaa vain hioa perusasiat uudelleen. Keskusteltuamme siitä, kuinka olla hyvä oppija matematiikassa, tämä artikkeli opettaa sinulle matematiikan perusasiat ja antaa sinulle peruselementit, jotka sinun on opittava jokaisessa harjoituksessa. Tämän jälkeen tässä artikkelissa käsitellään aritmeettisen oppimisen perusteita, jotka auttavat sekä peruskoululaisia että kaikkia, jotka haluavat oppia tämän tieteenalueen perusteet.
Vaihe
Osa 1/6: Avaimet hyvään matematiikan opiskelijaksi

Vaihe 1. Esitä luokassa
Kun kaipaat luokkaa, sinun on opittava käsitteitä luokkatovereiltasi tai oppikirjastasi. Et koskaan saa tekstiyhteenvetoa ystävältäsi niin paljon kuin opettajalta.
- Tule luokkaan ajoissa. Tule sen sijaan hieman aikaisin ja avaa muistikirja oikeaan paikkaan, avaa oppikirjasi ja ota laskin ulos, jotta olet valmis aloittamaan, kun opettajasi on valmis opettamaan.
- Kieltäydy vain, jos olet sairas. Jos kaipaat todella luokkaa, pyydä luokkatovereitasi selvittämään, mistä opettaja puhui ja mitä läksyjä annettiin.

Vaihe 2. Työskentele opettajasi kanssa
Jos opettajasi käsittelee ongelmaa luokan edessä, työskentele opettajan kanssa käsittelemällä muistikirjasi ongelmaa.
- Varmista, että muistiinpanosi ovat selkeitä ja helppolukuisia. Älä vain kirjoita kysymyksiä. Kirjoita myös ylös kaikki opettajan sanomat asiat, jotka voivat parantaa ymmärrystäsi selitettävistä käsitteistä.
- Täytä opettajasi antamat esimerkkikysymykset. Kun opettaja kulkee luokan ympäri työskennellessäsi, vastaa esitettyihin kysymyksiin.
- Osallistu, kun opettaja ratkaisee ongelman. Älä odota, että opettaja soittaa sinulle. Tarjoa vastaus, kun tiedät vastauksen, ja nosta kätesi esittääksesi kysymyksen, jos olet epävarma opetettavasta materiaalista.

Vaihe 3. Tee läksyt samana päivänä, kun kotitehtäväsi annetaan
Jos teet läksyt samana päivänä, käsite on vielä tuore mielessäsi. Joskus kotitehtävien suorittaminen samana päivänä ei ole mahdollista. Varmista, että läksyt on tehty ennen kuin lähdet luokalle.

Vaihe 4. Työskentele luokan ulkopuolella, jos tarvitset apua
Käy opettajan luona taukojen aikana tai toimistoaikana.
- Jos koulullasi on matematiikkakeskus, ota selvää sen aukioloajoista ja pyydä apua.
- Liity opintoryhmään. Hyvässä opintoryhmässä on yleensä 4 tai 5 henkilöä, joilla on erilaiset kyvyt. Jos olet matematiikan "C" -opiskelija, liity 2 tai 3 oppilaan ryhmään, jolla on "A" tai "B" arvosanoja, jotta voit parantaa taitojasi. Vältä liittymistä oppilasryhmään, jonka arvosanat ovat alemmat kuin sinun.
Osa 2/6: Matematiikan oppiminen koulussa

Vaihe 1. Aloita laskemisesta
Useimmissa kouluissa opiskelijat oppivat laskutoimituksen peruskoulussa. Aritmetiikka kattaa yhteenlaskun, vähentämisen, kertomisen ja jaon perusteet.
- Harjoittele kysymyksiä. Aritmeettisten tehtävien tekeminen uudestaan ja uudestaan on paras tapa muistaa perusasiat oikein. Etsi ohjelmistoja, jotka voivat tarjota sinulle laajan valikoiman erilaisia matemaattisia ongelmia. Etsi myös nopeuden parantamiseen liittyviä aikatauluihin liittyviä ongelmia.
- Löydät myös aritmeettisia ongelmia verkossa ja voit ladata aritmeettisia sovelluksia mobiililaitteellesi.

Vaihe 2. Jatka esialgebraa
Tämä harjoitus tarjoaa sinulle peruselementtejä, joita tarvitset ratkaisemaan algebran ongelmat myöhemmin.
- Opi murtoluvuista ja desimaaleista. Opit lisäämään, vähentämään, kertomaan ja jakamaan murtoja ja desimaaleja. Mitä tulee murtoihin, opit vähentämään murtoja ja kääntämään yhdistettyjä numeroita. Desimaalien suhteen ymmärrät paikka -arvot ja pystyt käyttämään desimaaleja tarinaongelmissa.
- Opi suhteista, mittasuhteista ja prosentteista. Nämä käsitteet auttavat sinua oppimaan vertaamaan.
- Esittele perusgeometria. Opit 3D -muotoja ja käsitteitä. Opit myös käsitteitä, kuten alueen, kehän, tilavuuden ja pinta -alan sekä tietoja yhdensuuntaisista ja kohtisuorasta viivoista ja kulmista.
- Ymmärtää joitain perustilastoja. Esialgebrassa esittelysi tilastoihin sisältää yleensä visuaaleja, kuten kaavioita, pistekaavioita, leimakaavioita ja histogrammeja.
- Opi algebran perusteet. Tämä sisältää käsitteitä, kuten muuttujia sisältävien yksinkertaisten yhtälöiden ratkaiseminen, ominaisuuksien, kuten jakautuvan ominaisuuden, oppiminen, yksinkertaisten yhtälöiden piirtäminen ja eriarvoisuuden ratkaiseminen.
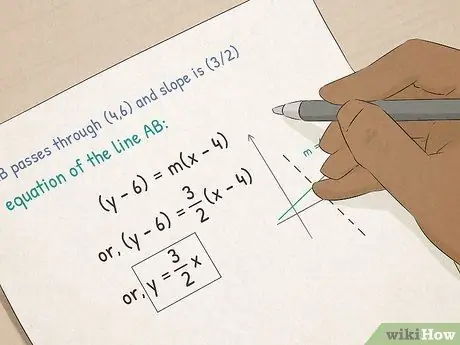
Vaihe 3. Siirry algebralle I
Ensimmäisen algebran vuoden aikana opit algebran perussymboleista. Opit myös:
- Ratkaise muuttujia sisältävät yhtälöt ja eriarvoisuudet. Opit ratkaisemaan nämä ongelmat paperilla ja ratkaisemaan ne kuvilla.
- Ratkaise tarinaongelmat. Tulet yllättymään siitä, kuinka monta arjen ongelmaa kohtaat tulevaisuudessa, mikä edellyttää kykyä ratkaista algebrallisia tarinaongelmia. Esimerkiksi algebran avulla voit selvittää pankkitilillesi tai sijoituksellesi ansaitsemasi koron. Voit myös käyttää algebraa selvittääksesi, kuinka kauan sinun pitäisi matkustaa autosi nopeuden perusteella.
- Työskentele eksponenttien kanssa. Kun alat ratkaista polynomiyhtälöitä (lausekkeita, jotka sisältävät numeroita ja muuttujia), ymmärrät eksponenttien käytön. Tämä sisältää todennäköisesti harjoituksia, joilla on tieteellinen merkintä. Kun olet oppinut eksponentit, voit oppia lisäämään, vähentämään, kertomaan ja jakamaan polynomi -lausekkeita.
- Ratkaise neliö- ja neliöjuuriongelmat. Kun hallitset tätä aihetta, voit muistaa monien numeroiden neliöt. Voit myös työskennellä yhtälöillä, joilla on neliöjuuret.
- Ymmärtää funktiot ja kaaviot. Algebrassa opit graafisista yhtälöistä. Opit laskemaan suoran kaltevuuden, asettamaan yhtälön piste-kaltevuusmuotoon ja laskemaan suoran x-ja-viipale kulmakerroinlomakkeen avulla.
- Ota selvää yhtälöjärjestelmästä. Joskus sinulle annetaan kaksi erilaista yhtälöä muuttujilla x ja y, ja sinun on ratkaistava x tai y molemmille yhtälöille. Onneksi opit paljon temppuja näiden yhtälöiden ratkaisemiseksi, mukaan lukien piirtäminen, korvaaminen ja lisääminen.

Vaihe 4. Tutki geometriaa
Geometriassa opit viivojen, segmenttien, kulmien ja muotojen ominaisuuksista.
- Muistat useita lauseita ja seurauksia, jotka auttavat sinua ymmärtämään geometrian sääntöjä.
- Opit laskemaan ympyrän alueen, käyttämään Pythagoraan lauseita ja löytämään erityisen kolmion kulmien ja sivujen välisen suhteen.
- Näet monia geometriakysymyksiä tulevissa standardoiduissa testeissä, kuten SAT, ACT ja GRE.
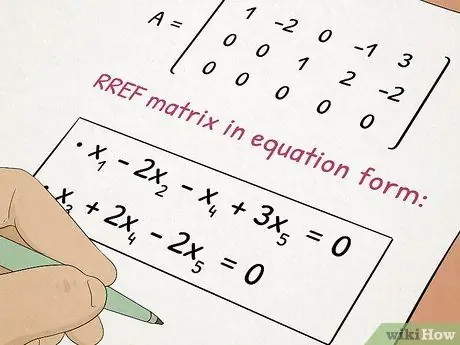
Vaihe 5. Ota Algebra II -luokka
Algebra II perustuu Algebra I: ssä opittuihin käsitteisiin ja lisää samalla monimutkaisia aiheita, kuten toisen asteen yhtälöitä ja matriiseja.
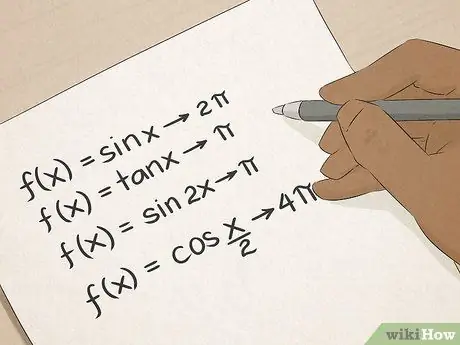
Vaihe 6. Master -trigonometria
Tiedät trigonometriset termit: sini, kosini, tangentti ja niin edelleen. Trigonometria opettaa sinulle monia käytännön tapoja laskea kulmat ja viivanpituudet, ja nämä taidot ovat korvaamattomia rakennusalalla, arkkitehtuurissa, suunnittelussa tai maanmittauksessa työskenteleville.
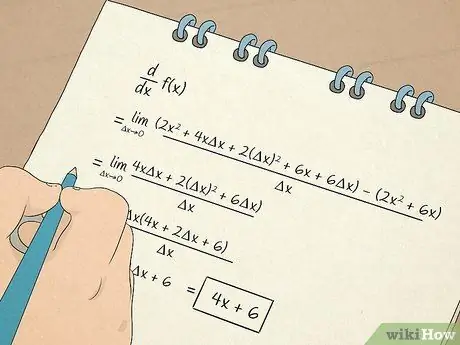
Vaihe 7. Tee laskutoimitukset
Laskenta voi kuulostaa pelottavalta, mutta se on loistava työkalu joko numeroiden käyttäytymisen tai ympäröivän maailman ymmärtämiseen.
- Laskenta opettaa sinulle toimintoja ja rajoja. Näet hyödyllisten funktioiden lukukäyttäytymisen, mukaan lukien e^x ja logaritmiset funktiot.
- Opit myös laskemaan ja käsittelemään johdannaisia. Ensimmäinen derivaatta antaa sinulle tietoa, joka perustuu yhtälön tangenttilinjan kaltevuuteen. Esimerkiksi johdannainen kertoo nopeuden, jolla jokin muuttuu epälineaarisessa tilanteessa. Toinen derivaatta kertoo, lisääntyykö vai pieneneekö funktio tietyn ajan kuluessa, jotta voit määrittää funktion koveruuden.
- Integraalit opettavat kuinka lasketaan käyrän alla oleva alue ja sen tilavuus.
- Lukion laskenta päättyy yleensä jaksoihin ja sekvensseihin. Vaikka opiskelijat eivät näe monia piirien sovelluksia, piirit ovat tärkeitä differentiaaliyhtälöitä opiskeleville.
Osa 3/6: Matematiikan perusteet-Master-lisäys

Vaihe 1. Aloita+1 -faktoilla
Lisäämällä numeroon 1 saat numerorivin korkeimman numeron. Esimerkiksi 2 + 1 = 3.
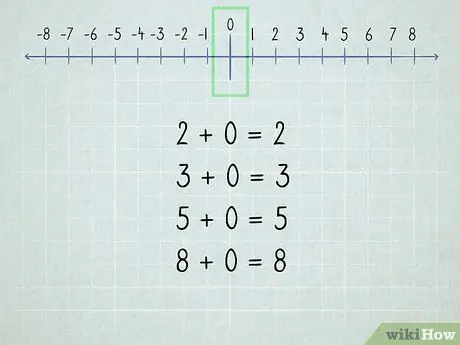
Vaihe 2. Ymmärrä nolla
Kaikki nollaan lisätyt numerot ovat sama luku, koska "nolla" tarkoittaa "ei mitään".

Vaihe 3. Opi kaksinkertaiset numerot
Useita numeroita on ongelma, johon liittyy kahden yhtä suuren luvun lisääminen. Esimerkiksi 3 + 3 = 6 on esimerkki yhtälöstä, joka sisältää useita numeroita.

Vaihe 4. Tutustu muihin lisäratkaisuihin kartoituksen avulla
Alla olevassa esimerkissä opit kartoittamalla, mitä tapahtuu, kun lisäät 3, 5, 2 ja 1. Kokeile "lisää 2" -ongelmaa itse.

Vaihe 5. Jatka, kunnes luku on yli 10
Opi lisäämään kolme numeroa yhteen saadaksesi suurempi kuin 10.
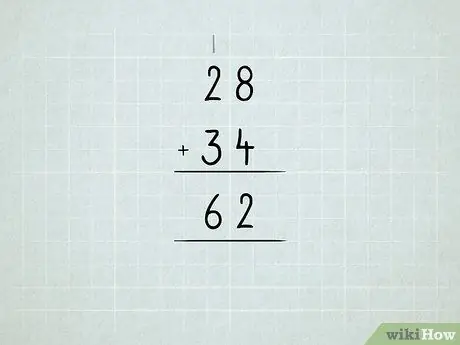
Vaihe 6. Lisää suuret numerot yhteen
Opi yksiköiden ryhmittelystä kymmeniin, kymmenistä satoihin ja niin edelleen.
- Lisää ensin oikeassa sarakkeessa olevat numerot. 8 + 4 = 12, mikä tarkoittaa, että sinulla on 1 numero 10 ja 2 numero 1. Kirjoita numero 2 yksikkösarakkeen alle.
-
Kirjoita numero 1 kymmenien sarakkeeseen.
-
Lisää kymmeniä sarakkeita kokonaisuudessaan.
Osa 4/6: Matemaattiset perusteet-vähentämisstrategiat

Vaihe 1. Aloita "taaksepäin 1 numero
Jos vähennät numerosta yhden, saat yhden numeron takaisin. Esimerkiksi 4 - 1 = 3.

Vaihe 2. Opi vähentämään kaksoislukuja
Esimerkiksi lisäät numerot 5 + 5 saadaksesi 10. Kirjoita yhtälö taaksepäin saadaksesi 10 - 5 = 5.
- Jos 5 + 5 = 10, niin 10-5 = 5.
-
Jos 2 + 2 = 4, niin 4-2 = 2.

Vaihe 3. Muista perhe
Esimerkiksi:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Vaihe 4. Etsi puuttuvat numerot
Esimerkiksi _ + 1 = 6 (vastaus on 5).

Vaihe 5. Muista vähennys tosiasiaksi 20

Vaihe 6. Harjoittele yhden numeron vähentämistä kaksinumeroisesta numerosta ilman lainaamista
Vähennä Yksit -sarakkeen numerot ja vähennä kymmenien sarakkeen numeroita.
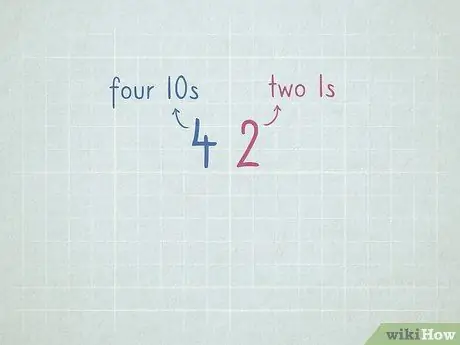
Vaihe 7. Harjoittele paikka -arvoa ja valmistaudu vähentämään lainaamalla
- 32 = 3 numeroa 10 ja 2 numeroa 1.
- 64 = 6 numeroa 10 ja 4 numeroa 1.
- 96 = _ numero 10 ja _ numero 1.
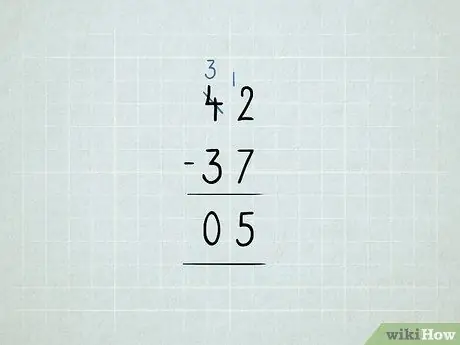
Vaihe 8. Vähennä lainaamalla
- Haluat vähentää 42 - 37. Aloita vähentämällä 2-7 yksikkösarakkeessa. Kävi ilmi, se ei toiminut!
-
Lainaa numero 10 kymmenien sarakkeesta ja aseta se sarakkeeseen Yksit. Nyt sinulla on 3 10: tä 4 10: n sijasta. Nyt sinulla on 12 1: tä 2 1: n sijasta.
-
Vähennä ensin yksikkösarakkeesi: 12 - 7 = 5. Tarkista sitten kymmenien sarake. Koska 3 - 3 = 0, sinun ei tarvitse kirjoittaa numeroa 0. Vastauksesi on 5.
Osa 5/6: Matematiikan perusteet-Mestarin kertolasku

Vaihe 1. Aloita numerolla 1 ja numerolla 0
Kaikki luvut, jotka kerrotaan yhdellä, ovat samat kuin itse luku. Mikä tahansa luku kerrottuna 0: lla on nolla.

Vaihe 2. Muista kertolasku

Vaihe 3. Harjoittele yksinumeroisten kerto -ongelmien kanssa

Vaihe 4. Kerro 2-numeroinen luku 1-numeroisella numerolla
- Kerro oikeassa alakulmassa oleva numero oikealla ylhäällä.
-
Kerro oikean alakulman numero vasemman yläkulman numerolla.
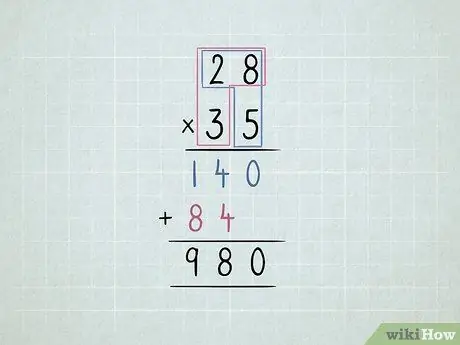
Vaihe 5. Kerro 2 2-numeroista numeroa
- Kerro oikeassa alakulmassa oleva numero oikealla ylänumerolla ja sitten vasemman yläkulman numerolla.
-
Siirrä toinen rivi yksi numero vasemmalle.
- Kerro vasen alareunan numero oikealla ylhäällä ja sitten vasemman yläkulman numero.
-
Lisää kaikki sarakkeet.
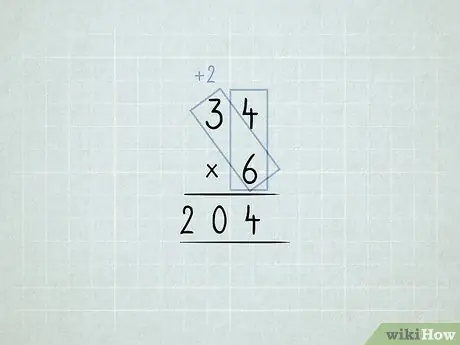
Vaihe 6. Kerro ja ryhmittele sarakkeet uudelleen
- Haluat kertoa 34 x 6. Aloitat kertomalla yksikkösarakkeen (4 x 6), mutta yksikkösarakkeessa ei voi olla 24 1: tä.
-
Tallenna 4 1 yksiköt -sarakkeeseen. Siirry 2 10 sekuntia kymmenien sarakkeeseen.
-
Kerro 6 x 3, joka on 18. Lisää 2 siirtämääsi, joka on 20.
Osa 6/6: Matemaattiset perusteet-paljasta divisioonan ongelmat

Vaihe 1. Ajattele jakamista eikä kertomista
#* Jos 4 x 4 = 16, niin 16 /4 = 4.
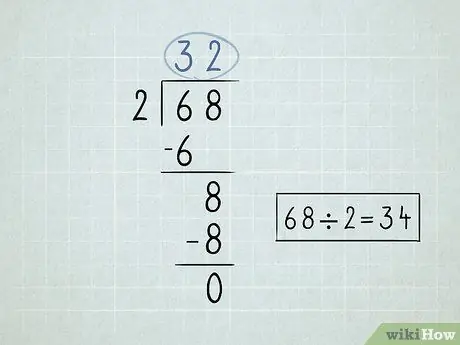
Vaihe 2. Kirjoita jako -ongelmasi muistiin
- Jaa jakosymbolin tai jakajan vasemmalla puolella oleva numero jakajan symbolin alla olevalla ensimmäisellä numerolla. Koska 6/2 = 3, kirjoitat luvun 3 jakosymbolin yläpuolelle.
-
Kerro jakosymbolin yläpuolella oleva luku jakajalla. Laske tulos ensimmäisen numeron alareunaan jakosymbolin alla. Koska 3 x 2 = 6, alennat numeroa 6 alaspäin.
- Vähennä kaksi kirjoittamaasi numeroa. 6 - 6 = 0. Voit jättää 0 tyhjäksi, koska et yleensä aloita numeroita 0: lla.
-
Tuo alas toinen numero, joka on jakosymbolin alapuolella.
- Jaa laskemasi numero jakajalla. Tässä tapauksessa 8 /2 = 4. Kirjoita jakosymbolin yläpuolelle numero 4.
-
Kerro oikea ylänumero jakajalla ja laske numero alas. 4 x 2 = 8.
-
Vähennä nuo numerot. Lopullinen vähennys palauttaa nollaa, mikä tarkoittaa, että olet ratkaissut ongelman. 68 x 2 = 34.

Vaihe 3. Laske myös loput
Osa jakajista ei ole täysin jaettu muihin numeroihin. Jos olet suorittanut viimeisen vähennyslaskun ja sinulla ei ole enempää laskettavia numeroita, viimeinen luku on loppuosa.






