3 tapaa laskea höyrynpaine

2024 Kirjoittaja: Jason Gerald | [email protected]. Viimeksi muokattu: 2024-02-01 14:13

Oletko koskaan jättänyt vesipullon kuumalle auringolle muutamaksi tunniksi ja kuullut pienen "sihisevän" äänen avatessasi sen? Tämä johtuu periaatteesta, jota kutsutaan höyrynpaineeksi. Kemiassa höyrynpaine on paine, joka kohdistuu suljetun astian seiniin, kun siinä oleva kemiallinen aine haihtuu (muuttuu kaasuksi). Löydä höyrynpaine tietyssä lämpötilassa käyttämällä Clausius-Clapeyronin yhtälöä: ln (P1/P2) = (ΔH_höyryä/R) ((1/T2) - (1/T1)).

Vaihe

Menetelmä 1/3: Clausius-Clapeyron-yhtälön käyttäminen

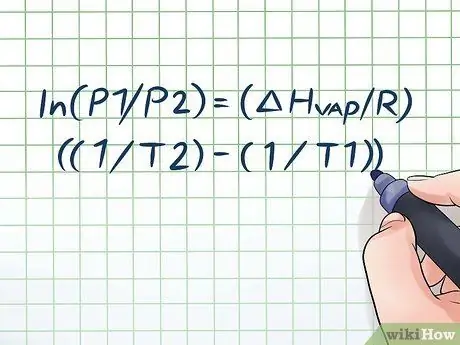
Vaihe 1. Kirjoita Clausius-Clapeyron-yhtälö muistiin

Kaavaa, jota käytetään höyrynpaineen laskemiseen höyrynpaineen muutoksen kanssa ajan mittaan, kutsutaan Clausius -Clapeyron -yhtälöksi (nimetty fyysikoiden Rudolf Clausiuksen ja Benoît Paul mile Clapeyronin mukaan.) Tämä on pohjimmiltaan kaava, jota tarvitset ratkaisemaan useimmat ongelmatyypit Höyrynpaineen kysymyksiä löytyy usein fysiikan ja kemian tunneilta. Kaava on seuraava: ln (P1/P2) = (ΔH_höyryä/R) ((1/T2) - (1/T1)). Tässä kaavassa muuttujat edustavat:

• H_höyryä:

  Nesteen höyrystymisen entalpia. Tämä entalpia löytyy yleensä kemian oppikirjan takana olevasta taulukosta.

• R:

  Todellinen/universaali kaasuvakio, tai 8,314 J/(K × Mol).

• Kysymys 1:

  Lämpötila, jossa höyrynpaine tunnetaan (tai alkulämpötila).

• T2:

  Lämpötila, jossa höyrynpaine on tuntematon/haluttu löytää (tai lopullinen lämpötila).

• P1 ja P2:

  Höyrynpaine lämpötiloissa T1 ja T2.

Vaihe 2. Syötä tuntemasi muuttujat

Clausius-Clapeyronin yhtälö näyttää monimutkaiselta, koska siinä on paljon erilaisia muuttujia, mutta se ei oikeastaan ole niin vaikeaa, jos sinulla on oikeat tiedot. Useimmat perushöyrynpaineongelmat luettelevat kaksi lämpötila -arvoa ja yhden painearvon tai kaksi paine -arvoa ja yhden lämpötila -arvon - kun ymmärrät tämän, tämän yhtälön ratkaiseminen on erittäin helppoa.

• Oletetaan esimerkiksi, että meille kerrotaan, että meillä on säiliö täynnä nestettä 295 K: ssa, jonka höyrynpaine on 1 atmosfääri (atm). Kysymyksemme on: Mikä on höyrynpaine 393 K: ssa? Meillä on kaksi lämpötila-arvoa ja yksi painearvo, joten voimme löytää muut painearvot käyttämällä Clausius-Clapeyron-yhtälöä. Liittämällä muuttujamme, saamme ln (1/P2) = (ΔH_höyryä/R) ((1/393) - (1/295)).
• Huomaa, että Clausius-Clapeyron -yhtälölle on aina käytettävä lämpötila-arvoa Kelvin. Voit käyttää mitä tahansa painearvoa, kunhan P1- ja P2 -arvot ovat samat.

Vaihe 3. Anna vakiosi

Clausius-Clapeyron -yhtälössä on kaksi vakiota: R ja H_höyryä. R on aina 8,314 J/(K × Mol). Kuitenkin H._höyryä (höyrystymisen entalpia) riippuu aineesta, jonka höyrynpainetta etsit. Kuten edellä on mainittu, löydät yleensä H: n arvot_höyryä eri aineille kemian tai fysiikan oppikirjan takana tai verkossa (kuten esimerkiksi täällä.)

• Esimerkissämme oletetaan, että nesteemme on puhdas vesi.

  Jos tarkastelemme taulukkoa, H: n arvot_höyryä, huomaamme, että H._höyryä puhdasta vettä on noin 40,65 KJ/mol. Koska H -arvo on jouleina eikä kilojouleina, voimme muuntaa sen arvoksi 40650 J/mol.

• Kytkemällä vakiomme, saamme ln (1/P2) = (40650/8, 314) ((1/393) - (1/295)).

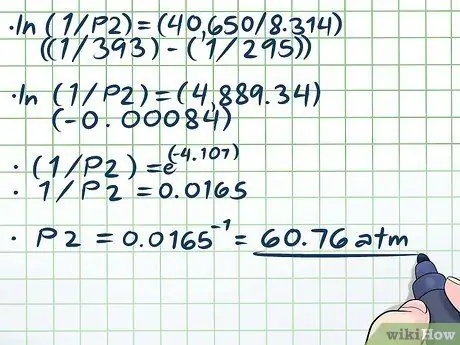
Vaihe 4. Ratkaise yhtälö

Kun olet sisällyttänyt kaikki muuttujat yhtälöön paitsi etsimäsi, jatka yhtälön ratkaisemista tavallisen algebran sääntöjen mukaisesti.

• Ainoa vaikea osa yhtälömme ratkaisemisessa (ln (1/P2) = (40650/8, 314) ((1/393) - (1/295))) ratkaisee luonnollisen lokin (ln). Jos haluat poistaa luonnollisen lokin, käytä yhtälön molempia puolia eksponentteina matemaattiselle vakioon e. Toisin sanoen, ln (x) = 2 → e^{ln (x)} = e² → x = e².

• Nyt ratkaistaan yhtälö:
• ln (1/P2) = (40650/8, 314) ((1/393) - (1/295))
• ln (1/P2) = (4889, 34) (-0, 00084)
• (1/P2) = e^{(-4, 107)}
• 1/P2 = 0,0165

• P2 = 0,0165^-1 = 60, 76 atm.

  Tämä on järkevää - suljetussa astiassa lämpötilan nostaminen lähes 100 asteeseen (lähes 20 asteeseen kiehumispisteen yläpuolelle) tuottaa paljon höyryä ja lisää painetta nopeasti.

Menetelmä 2/3: Höyrynpaineen määrittäminen liuenneella liuoksella

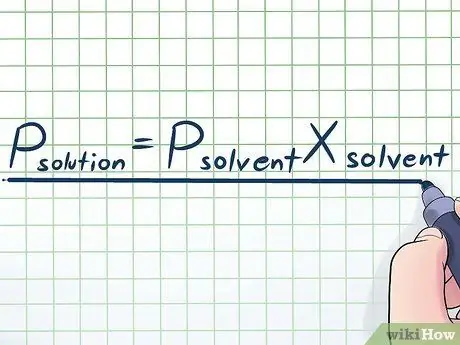
Vaihe 1. Kirjoita muistiin Raoultin laki

Tosielämässä työskentelemme harvoin puhtaan nesteen kanssa - yleensä työskentelemme nesteen kanssa, joka on useiden eri aineiden seos. Jotkut yleisimmin käytetyistä seoksista valmistetaan liuottamalla pieni määrä tiettyä kemikaalia, jota kutsutaan liuenneeksi aineeksi, moniin kemikaaleihin, joita kutsutaan liuottimeksi liuoksen valmistamiseksi. Näissä tapauksissa on hyödyllistä tietää yhtälö nimeltä Raoult's Law (nimetty fyysikon François-Marie Raoult'n mukaan), joka on kirjoitettu näin: P_liukoinen= P_liuotinX_liuotin. Tässä kaavassa muuttujat edustavat;

• P_liukoinen:

  Koko liuoksen höyrynpaine (kaikki elementit yhdistettynä)

• P_liuotin:

  Liuottimen höyrynpaine

• X_liuotin:

  Liuottimen moolifraktio

• Älä huolestu, jos et tunne termejä, kuten moolifraktio - selitämme ne seuraavissa vaiheissa.

Vaihe 2. Määritä liuotin ja liuennut aine liuoksessa

Ennen kuin voit laskea sekoitetun nesteen höyrynpaineen, sinun on tunnistettava käyttämäsi aineet. Muistutuksena, että liuos muodostuu, kun liuennut aine liukenee liuottimeen.

• Käytämme tämän osan yksinkertaisia esimerkkejä havainnollistamaan käsitteitä, joista keskustelemme. Oletetaan esimerkiksi, että haluamme löytää sokerisiirapin höyrynpaineen. Perinteisesti sokerisiirappi on vesiliukoinen sokeri (suhde 1: 1), joten voimme sanoa sen sokeri on liuennut aineemme ja vesi liuottimemme.
• Huomaa, että sakkaroosin (pöytäsokeri) kemiallinen kaava on C₁₂H₂₂O₁₁. Tämä kemiallinen kaava on erittäin tärkeä.

Vaihe 3. Etsi liuoksen lämpötila

Kuten edellä Clausius Clapeyron -osiossa näimme, nesteen lämpötila vaikuttaa sen höyrynpaineeseen. Yleensä mitä korkeampi lämpötila, sitä suurempi höyrynpaine - lämpötilan noustessa enemmän nestettä haihtuu ja muodostaa höyryä, mikä lisää säiliön painetta.

Esimerkissämme sanotaan, että sokerisiirapin lämpötila on tässä vaiheessa 298 K. (noin 25 C).

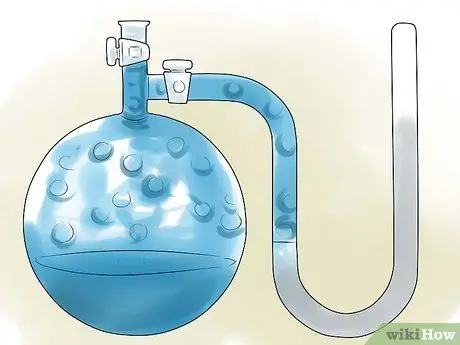
Vaihe 4. Etsi liuottimen höyrynpaine

Kemiallisilla vertailumateriaaleilla on yleensä höyrynpainearvot monille yleisesti käytetyille aineille ja yhdisteille, mutta nämä painearvot ovat yleensä päteviä vain, jos aineen lämpötila on 25 C/298 K tai sen kiehumispiste. Jos liuoksessasi on jokin näistä lämpötiloista, voit käyttää viitearvoa, mutta jos ei, sinun on löydettävä höyrynpaine kyseisessä lämpötilassa.

• Clausius -Clapeyron voi auttaa - käytä vertailuhöyrynpainetta ja 298 K (25 C) P1: lle ja T1: lle.
• Esimerkissämme seoksen lämpötila on 25 ° C, joten voimme helposti käyttää helppotaulukkoa. Tiedämme, että 25 ° C: ssa veden höyrynpaine on 23,8 mm HG

Vaihe 5. Etsi liuottimen mooliosuus

Viimeinen asia, joka meidän on tehtävä ennen kuin voimme ratkaista tämän, on löytää liuottimemme mooliosuus. Moolijakeen löytäminen on helppoa: muunna yhdisteet mooleiksi ja etsi sitten kunkin yhdisteen prosenttiosuus aineen moolien kokonaismäärästä. Toisin sanoen kunkin yhdisteen mooliosuus on yhtä suuri kuin (moolia yhdistettä)/(moolien kokonaismäärä aineessa).

• Oletetaan reseptimme sokerisiirapin käyttöön 1 litra (L) vettä ja 1 litra sakkaroosia (sokeria).

  Tässä tapauksessa meidän on löydettävä kunkin yhdisteen moolimäärä. Tätä varten löydämme kunkin yhdisteen massan ja käytämme sitten aineen moolimassaa sen muuntamiseksi mooleiksi.

• Massa (1 l vettä): 1000 grammaa (g)
• Massa (1 l raakasokeria): noin 1056, 8 g
• Moolit (vesi): 1000 grammaa × 1 mol/18,015 g = 55,51 mol
• Moolit (sakkaroosi): 1056, 7 grammaa × 1 mol/342,2965 g = 3,08 moolia (huomaa, että sakkaroosin moolimassa löytyy sen kemiallisesta kaavasta, C₁₂H₂₂O₁₁.)
• Moleja yhteensä: 55,51 + 3,08 = 58,59 mol
• Veden mooliosuus: 55, 51/58, 59 = 0, 947

Vaihe 6. Viimeistele

Lopuksi meillä on kaikki mitä tarvitsemme ratkaistaksemme Raoultin lain yhtälön. Tämä osa on erittäin helppo: lisää vain muuttujien arvot yksinkertaistetussa Raoult's Law -yhtälössä tämän osan alussa (P_liukoinen = P_liuotinX_liuotin).

• Kirjoittamalla arvomme, saamme:
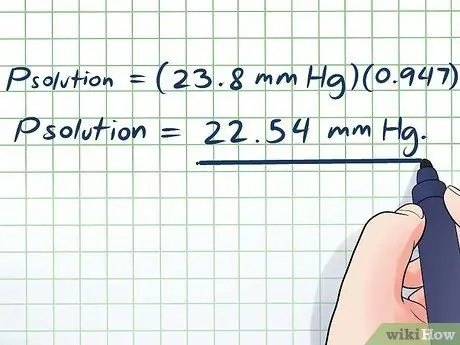
• P_ratkaisu = (23,8 mm Hg) (0, 947)

• P_ratkaisu = 22,54 mm Hg.

  Tulos on järkevä - moolimuodossa sokeria liukenee hyvin vähän veteen (tosielämässä molempien ainesosien tilavuus on sama), joten höyrynpaine laskee vain hieman.

Tapa 3/3: Höyrynpaineen määrittäminen erityistapauksissa

Vaihe 1. Ole varovainen normaaleissa lämpötila- ja paineolosuhteissa

Tutkijat käyttävät usein joukkoa lämpötila- ja painearvoja helppokäyttöisenä "standardina". Näitä arvoja kutsutaan normaalilämpötilaksi ja paineeksi (tai STP). Höyrynpaineongelmat viittaavat usein STP -olosuhteisiin, joten on tärkeää muistaa nämä arvot. STP -arvot määritellään seuraavasti:

• Lämpötila: 273, 15 K. / 0 C / 32 F
• Paine: 760 mm Hg / 1 atm / 101, 325 kilopascalia

Vaihe 2. Järjestä Clausius-Clapeyronin yhtälö löytääksesi muut muuttujat

Esimerkissämme osassa 1 huomasimme, että Clausius -Clapeyronin yhtälö on erittäin hyödyllinen puhtaiden aineiden höyrynpaineen löytämiseksi. Kaikki kysymykset eivät kuitenkaan pyydä sinua etsimään P1 tai P2 - monet pyytävät sinua löytämään lämpötila -arvon tai joskus jopa H -arvon._höyryä. Onneksi näissä tapauksissa vastauksen saaminen on yksinkertaisesti kyse yhtälön uudelleenjärjestelystä siten, että ratkaisemasi muuttujat ovat erillään yhtäläisyysmerkin toisella puolella.

• Oletetaan esimerkiksi, että meillä on tuntematon neste, jonka höyrynpaine on 25 torria 273 K: ssa ja 150 torria 325 K: ssa, ja haluamme löytää tämän nesteen höyrystymisen entalpian (ΔH_höyryä). Voimme ratkaista sen seuraavasti:
• ln (P1/P2) = (ΔH_höyryä/R) ((1/T2) - (1/T1))
• (ln (P1/P2))/((1/T2) - (1/T1)) = (ΔH_höyryä/R)
• R × (ln (P1/P2))/((1/T2) - (1/T1)) = H_höyryä Kirjoitamme nyt arvomme:
• 8, 314 J/(K × Mol) × (-1, 79)/(-0, 00059) = H_höyryä
• 8, 314 J/(K × Mol) × 3033, 90 = H_höyryä = 25 223, 83 J/mol

Vaihe 3. Laske liuenneen aineen höyrynpaine, kun aine tuottaa höyryä

Yllä olevassa Raoult Law -esimerkissämme liuennut aineemme, sokeri, ei paina itseään normaalissa lämpötilassa (ajattele - milloin näit viimeksi sokerikulhon haihtuneen yläkaapistasi?) haihduta, tämä vaikuttaa höyrynpaineeseesi. Selvitämme tämän käyttämällä muokattua versiota Raoultin lain yhtälöstä: P_ratkaisu = (P._yhdisteX_yhdiste) Symboli sigma (Σ) tarkoittaa, että vastauksen saamiseksi meidän on vain laskettava yhteen eri yhdisteiden kaikki höyrynpaineet.

• Oletetaan esimerkiksi, että meillä on ratkaisu, joka koostuu kahdesta kemikaalista: bentseenistä ja tolueenista. Liuoksen kokonaistilavuus on 12 millilitraa (ml); 60 ml bentseeniä ja 60 ml tolueenia. Liuoksen lämpötila on 25 ° C ja näiden kemikaalien höyrynpaineet 25 ° C: ssa ovat 95,1 mmHg bentseenille ja 28,4 mmHg tolueenille. Näillä arvoilla löydät liuoksen höyrynpaineen. Voimme tehdä tämän seuraavasti käyttämällä kahden kemikaalin vakiotiheyttä, moolimassaa ja höyrynpainearvoja:
• Massa (bentseeni): 60 ml = 0,060 l & kertaa 876,50 kg/1000 L = 0,053 kg = 53 g
• Massa (tolueeni): 0,060 l & kertaa 866, 90 kg/1000 L = 0,052 kg = 52 g
• Moli (bentseeni): 53 g × 1 mol/78, 11 g = 0,679 mol
• Moolit (tolueeni): 52 g × 1 mol/92, 14 g = 0,564 mol
• Moleja yhteensä: 0,679 + 0,564 = 1,243
• Moolijae (bentseeni): 0,679/1, 243 = 0,546
• Moolifraktio (tolueeni): 0,564/1, 243 = 0,454
• Ratkaisu: P._ratkaisu = P_bentseeniX_bentseeni + P_tolueeniX_tolueeni
• P_ratkaisu = (95,1 mm Hg) (0, 546) + (28,4 mm Hg) (0, 454)
• P_ratkaisu = 51,92 mm Hg + 12,89 mm Hg = 64, 81 mm Hg

Vinkkejä

• Yllä olevan Clausius Clapeyron -yhtälön käyttämiseksi lämpötila on mitattava Kelvininä (kirjoitettuna K: nä). Jos lämpötila on Celsius, sinun on muunnettava se seuraavan kaavan avulla: T_k = 273 + T._c
• Yllä olevia menetelmiä voidaan käyttää, koska energia on täsmälleen verrannollinen käytetyn lämmön määrään. Nesteen lämpötila on ainoa ympäristötekijä, joka vaikuttaa höyrynpaineeseen.