Keskimääräisen nopeuden laskeminen: 12 vaihetta (kuvilla)

2024 Kirjoittaja: Jason Gerald | [email protected]. Viimeksi muokattu: 2024-02-01 14:13

Keskimääräisen nopeuden laskemiseksi tarvitset vain kokonaissiirtymän. tai sijainnin ja kokonaisajan muuttaminen. Muista, että nopeus laskee myös kohteen suunnan ja nopeuden, joten sisällytä vastaukseesi suunta, kuten "pohjoinen", "etu" tai "vasen". Jos nopeuslaskentaongelmaasi liittyy myös jatkuva kiihtyvyys, voit oppia nopean tavan löytää vastaus vieläkin helpommin.

Vaihe

Menetelmä 1: 2: Siirtymän ja ajan keskimääräisen nopeuden laskeminen

Vaihe 1. Muista, että nopeus sisältää sekä kohteen nopeuden että suunnan

Nopeus kuvaa nopeutta, jolla kohteen sijainti muuttuu. Tämä ei liity pelkästään kohteen liikkeen nopeuteen vaan myös sen suuntaan. "100 metriä sekunnissa etelään" on eri nopeusarvo kuin "100 metriä sekunnissa itään".

Suuntaa omaavia määriä kutsutaan vektorimääriksi '. Tämä määrä voidaan erottaa suunnattomasta määrästä, jota kutsutaan skalaariseksi suureksi, kirjoittamalla nuoli muuttujan yläpuolelle. Esimerkiksi merkintä v edustaa nopeutta, kun taas merkintä v ^→ edustaa nopeutta tai nopeutta + suuntaa. Tässä artikkelissa käytetty v -merkintä edustaa nopeutta.
Tieteellisissä ongelmissa sinun tulisi käyttää etäisyyksiä mittarien tai muiden metristen yksiköiden avulla, kun taas jokapäiväisiin tarkoituksiin voit käyttää mitä tahansa haluamaasi yksikköä.

Vaihe 2. Etsi koko siirtymäarvo

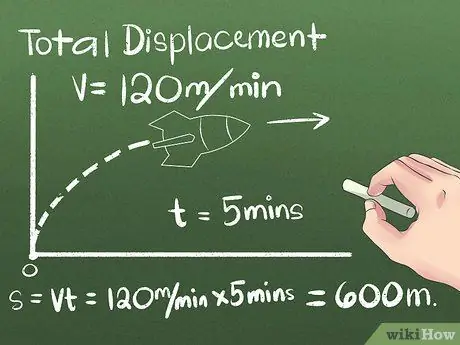
Siirtymä on muutos kohteen sijainnissa tai etäisyydessä ja suunnassa sen aloitus- ja lopetuspisteiden välillä. Suunta, johon kohde liikkuu ennen lopullisen sijaintinsa saavuttamista, voidaan jättää huomiotta, koska vain lähtö- ja päätepisteiden välinen etäisyys otetaan huomioon. Ensimmäisessä esimerkissä käytämme objektia, joka liikkuu vakionopeudella yhteen suuntaan:

Oletetaan, että raketti liikkuu pohjoiseen 5 minuutin ajan tasaisella nopeudella 120 metriä minuutissa. Laske lopullinen sijainti kaavalla s = vt tai käytä käytännön ajattelua raketin sen jälkeen kulkeman matkan (5 minuuttia) (120 metriä/minuutti) = 600 metriä pohjoiseen lähtökohdasta.
Jos ongelma liittyy jatkuvaan kiihtyvyyteen, voit ratkaista sen s = vt + at²tai etsi vastaus käyttämällä toisessa osassa kuvattua lyhyttä menetelmää.

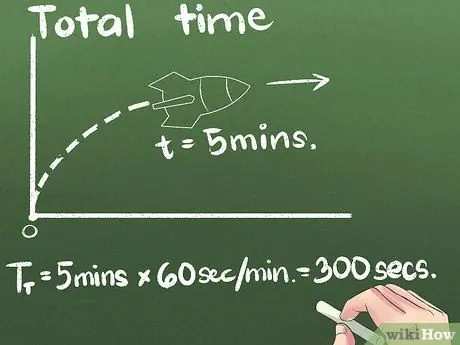
Vaihe 3. Etsi kokonaisaika

Esimerkissämme raketti liikkuu eteenpäin 5 minuuttia. Voit ilmaista keskinopeuden millä tahansa ajan yksiköllä, mutta toinen on kansainvälinen tieteellinen standardiyksikkö. Muutamme sekunnin yksiköitä tässä esimerkissä: (5 minuuttia) x (60 sekuntia/minuutti) = 300 sekuntia.

Jopa tieteellisissä ongelmissa, jos kysymyksessä käytetään tunti tai suurempi aikayksikkö, nopeuden laskeminen on ensin helpompaa ja lopullinen vastaus muunnetaan metreiksi sekunnissa

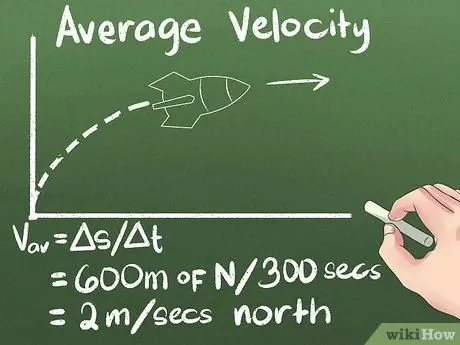
Vaihe 4. Laske keskimääräinen nopeus siirtymänä ajan mittaan

Jos tiedät, kuinka pitkälle kohde liikkuu ja kuinka kauan kestää päästä sinne, tiedät kuinka nopeasti se liikkuu. Joten käyttämässämme esimerkissä raketin keskimääräinen nopeus on (600 metriä pohjoiseen) / (300 sekuntia) = 2 metriä sekunnissa pohjoiseen.

Muista lisätä suunta (kuten "etu" tai "pohjoinen").
Kaavassa v_keskim = s/Δt. Deltasymboli tarkoittaa "muutosta", joten s/Δt tarkoittaa "asennon muutosta tietyn ajanjakson aikana".
Keskimääräinen nopeus voidaan kirjoittaa muodossa v_keskimtai v: nä, jonka yläpuolella on vaakasuora viiva.

Vaihe 5. Ratkaise monimutkaisempia ongelmia

Jos kohde muuttaa suuntaa tai nopeutta, älä hämmenny. Keskinopeus lasketaan edelleen "vain" kokonaistilavuudesta ja kokonaisajasta. Mitä alku- ja loppupisteiden välillä tapahtuu, voit jättää huomiotta. Seuraavassa on muutamia esimerkkejä esineestä, joka kulkee samalla siirtymällä ja kokonaisajalla ja siten samalla keskimääräisellä nopeudella:

Anna kävelee länteen nopeudella 1 metri/s 2 sekuntia, sitten kiihtyy yhtäkkiä 3 metriin sekunnissa ja jatkaa kävelyä länteen 2 sekuntia. Kokonaissiirtymä on (1 m/s länteen) (2 s) + (3 m/s länteen) (2 s) = 8 metriä länteen. Kokonaisaika on 2 sekuntia + 2 sekuntia = 4 sekuntia. Keskimääräinen nopeus on siis 8 metriä länteen/ 4 sekuntia = 2 metriä sekunnissa länteen.
Bart kävelee länteen nopeudella 5 metriä sekunnissa 3 sekuntia, sitten kääntyy ympäri ja kävelee itään nopeudella 7 metriä sekunnissa yhden sekunnin ajan. Voimme ajatella itäistä liikettä "negatiivisena liikkeenä länteen", joten kokonaissiirtymä on = (5 metriä/sek länteen) (3 sekuntia) + (-7 m/s länteen) (1 sek) = 8 metriä. Kokonaisaika = 4 sekuntia. Keskinopeus = 8 metriä länteen / 4 sekuntia = 2 metriä sekunnissa länteen.
Charlotte käveli 1 metriä pohjoiseen ja sitten 8 metriä länteen, sitten 1 metri etelään. Koko matkan suorittamiseen kuluva aika on 4 sekuntia. Piirrä kaavio paperille ja näet, että päätepiste on 8 metriä lähtöpisteestä länteen, joten tämä arvo on siirtymä. Kokonaisaika on 4 sekuntia, joten keskinopeus on 8 metriä länteen / 4 sekuntia = 2 metriä sekunnissa länteen.

Menetelmä 2/2: Kiinteän kiihtyvyyden keskimääräisen nopeuden laskeminen

Vaihe 1. Harkitse alkunopeutta ja jatkuvaa kiihtyvyyttä

Oletetaan, että ongelmamme on "Polkupyörä liikkuu oikealle nopeudella 5 m/s ja kiihtyy jatkuvasti 2 m/s². Jos tämä polkupyörä liikkuu 5 sekuntia, mikä on sen keskimääräinen nopeus?"

Jos yksikkö "mittari/sekunti²"Hämmentääksesi kirjoita se" metreinä sekunnissa "tai" metreinä sekunnissa "." 2 metrin/sekunnin/sekunnin kiihtyvyys tarkoittaa, että nopeus kasvaa 2 metriä sekunnissa joka sekunti.

Vaihe 2. Käytä kiihtyvyyttä löytääksesi lopullinen nopeus

Kiihtyvyys, merkitty merkinnällä a, on nopeuden (tai nopeuden) muutosnopeus. Nopeus kasvaa jatkuvasti. Voit piirtää taulukon kiihdytyksellä löytääksesi nopeuden eri aikoina polkupyörän matkan aikana. Meidän on luotava tämä taulukko ongelman lopetuspisteen löytämiseksi (t = 5 sekuntia), mutta luomme pidemmän taulukon, jotta voit helpommin ymmärtää tämän käsitteen:

Alkupisteessä (aika t = 0 sekuntia) polkupyörä liikkuu 5 metrin/s nopeudella.
1 sekunnin kuluttua (t = 1) polkupyörä liikkuu nopeudella 5 metriä sekunnissa + nopeudella = 5 metriä sekunnissa + (2 metriä sekunnissa)²) (1 sekunti) = 7 metriä/sekunti.
Kun t = 2, polkupyörä liikkuu oikealle nopeudella 5+ (2) (2) = 9 metriä/sek.
Kun t = 3, polkupyörä liikkuu oikealle nopeudella 5+ (2) (3) = 11 metriä/sek.
Kun t = 4, polkupyörä liikkuu oikealle nopeudella 5+ (2) (4) = 13 metriä/sek.
Kun t = 5, polkupyörä liikkuu oikealle nopeudella 5+ (2) (5) = 15 metriä/sekunti.

Vaihe 3. Käytä tätä kaavaa löytääksesi keskinopeuden

Jos ja "vain", jos kiihtyvyys on vakio, keskimääräinen nopeus on yhtä suuri kuin lopullisen ja alkunopeuden summan keskiarvo. (v_f +v_i)/2. Yllä olevassa esimerkkitehtävässämme polkupyörän alkuperäinen nopeus on v_i 5 metriä/sekunti. Laskennan jälkeen lopullinen nopeus on v_f 15 metriä/sekunti. Yhdistämällä nämä kaksi arvoa yhteen saadaan (15 metriä/sekunti + 5 metriä/sekunti)/2 = (20 metriä/sekunti)/2 = 10 metriä/sekunti oikeaan suuntaan.

Muista lisätä suunta, tässä tapauksessa "oikea".
Tämä termi voidaan kirjoittaa v₀ (nopeus hetkellä 0 tai alkunopeus) ja v (lopullinen nopeus).

Vaihe 4. Ymmärrä keskimääräisen nopeuden kaava intuitiivisesti

Keskimääräisen nopeuden löytämiseksi voimme käyttää nopeutta missä tahansa pisteessä ja löytää kaikkien niiden keskiarvon. (Tämä on keskiarvon määritelmä.) Koska tämä vaatii laskentaa tai ääretöntä aikaa, ymmärrä tämä kaava intuitiivisemmin. Jokaisen ajan ottamisen sijaan laske kahden ajankohdan keskimääräinen nopeus ja katso tulokset. Yksi ajankohta on lähellä ajon alkua, jossa pyörä kulkee hitaasti, ja toinen piste on lähellä päätepistettä, jossa pyörä kulkee nopeasti.

Vaihe 5. Testaa intuitiivinen teoria

Yllä olevan taulukon avulla voit määrittää nopeuden eri ajankohtina. Jotkut kriteerit täyttävät parit ovat (t = 0, t = 5), (t = 1, t = 4) tai (t = 2, t = 3). Voit halutessasi testata tätä kaavaa muilla t -arvoilla kuin kokonaislukuilla.

Valitsitpa minkä tahansa pisteparin, keskimääräinen nopeus on aina sama. Esimerkiksi ((5+15)/2), ((7+13)/2) tai ((9+11)/2) kaikki ovat 10 metriä sekunnissa oikealle

Vaihe 6. Suorita intuitiivinen selitys

Jos käytämme tätä menetelmää luettelon kanssa jokaisesta otetusta ajasta, laskemme edelleen matkan ensimmäisen puoliskon ja matkan jälkipuoliskon keskiarvon. Jokaisen puoliskon kattamiseen kuluva aika on sama, joten nopeus ei häviä laskemisen päätyttyä.

Koska kumpikin pari antaa saman tuloksen, myös näiden nopeuksien keskiarvo on arvoltaan sama. Esimerkissämme koko nopeus on "10 metriä sekunnissa oikealle" edelleen 10 metriä sekunnissa oikealle.
Voimme löytää tämän arvon laskemalla minkä tahansa parin keskiarvon, esimerkiksi alkunopeuden ja lopullisen nopeuden. Esimerkissämme nämä nopeudet saavutetaan t = 0 ja t = 5, ja ne voidaan laskea käyttämällä yllä olevaa kaavaa: (5+15)/2 = 10 metriä/sek oikealle.

Vaihe 7. Ymmärrä tämä kaava matemaattisesti

Jos pidät paremmin kaavoiksi kirjoitetuista todisteista, voit aloittaa kaavalla, joka laskee ajetun matkan olettaen jatkuvan kiihtyvyyden, ja johtaa kaava sieltä:

s = v_it + klo². (Teknisesti s ja t tai sijainnin muutos ja ajan muutos, mutta sinut ymmärretään myös, jos kirjoitat s ja t.)
Keskinopeus v_keskim määritelty s/t, joten syötä kaava muodossa s/t.
v_keskim = s/t = v_i + klo
Kiihtyvyys x aika on yhtä suuri kuin kokonaisnopeuden muutos, tai v_f - v_i. Joten voimme korvata kaavan "at" ja saada:
v_keskim = v_i + (v_f - v_i).
Yksinkertaista: v_keskim = v_i + v_f - v_i = v_i + v_f = (v_f +v_i)/2.

Vinkkejä

Nopeus eroaa nopeudesta, koska nopeus on vektorimäärä, kun taas nopeus on skalaarinen määrä. Vektorimäärät sisältävät sekä suunnan että suuruuden, kun taas skalaariset suuret sisältävät vain suuruuden.
Jos kohde liikkuu yhdessä ulottuvuudessa, kuten vasen-oikea, voit käyttää positiivista lukua edustaaksesi yhtä suuntaa (kuten oikeaa) ja negatiivista lukua edustamaan toista suuntaa (vasen). Kirjoita tämä merkintä sivusi yläreunaan, jotta se on selkeä työsi lukijoille.