- Kirjoittaja Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:14.
- Viimeksi muokattu 2025-01-23 12:17.
Normaalivoima on sen voiman suuruus, joka tarvitaan muiden voimien kieltämiseen missä tahansa skenaariossa. Paras tapa löytää se riippuu kohteen tilasta ja muuttujista. Jatka lukemista saadaksesi lisätietoja.
Vaihe
Menetelmä 1/5: Normaali tyyli levossa
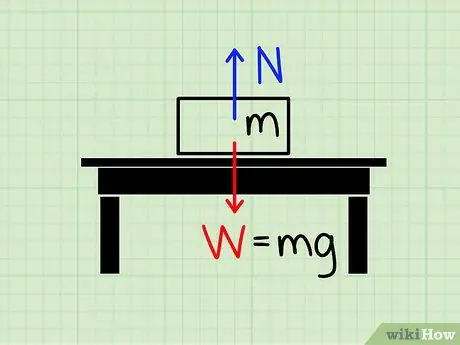
Vaihe 1. Ymmärrä normaalivoiman merkitys
Normaalivoima viittaa sen voiman suuruuteen, jota käytetään painovoiman kumoamiseen.
Kuvittele lohko levossa pöydällä. Painovoima vetää lohkoa kohti maata, mutta on selvää, että voima vaikuttaa estäen lohkoa murskaamasta pöytää ja putoamasta maahan. Voimaa, joka pysäyttää tämän lohkon painovoimasta huolimatta, kutsutaan normaali tyyli.
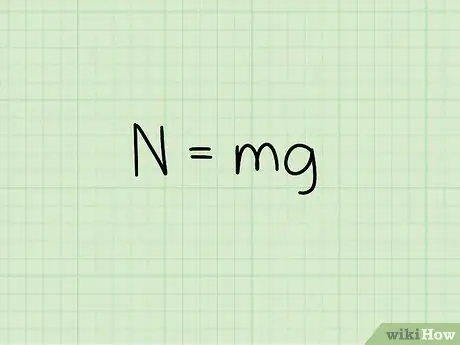
Vaihe 2. Tiedä normaalin voiman yhtälö levossa olevaan kohteeseen
Kun lasket esineen normaalivoiman, kun se on levossa tasaisella pinnalla, käytä kaavaa: N = m * g
- Tässä yhtälössä N symboloi normaalia tyyliä, m edustaa kohteen massaa, ja g kuvaa painovoiman aiheuttamaa kiihtyvyyttä.
- Jos esine on levossa tasaisella pinnalla ilman ulkoista voimaa, normaalivoima on yhtä suuri kuin kohteen paino. Jotta esine pysyy levossa, normaalivoiman on vastattava kohteeseen vaikuttavaa painovoimaa. Kohteeseen vaikuttava painovoima on kohteen paino tai kohteen massa kertaa painovoimasta johtuva kiihtyvyys.
- Esimerkki: Etsi 4,2 kg: n kappaleen normaalivoima.
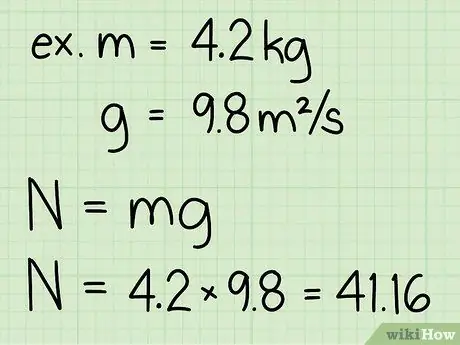
Vaihe 3. Kerro kohteen massa ja painovoimasta johtuva kiihtyvyys
Tämä kertolasku tuottaa kohteen painon, joka tietysti on yhtä suuri kuin kohteen normaalivoima levossa.
- Huomaa, että painovoiman aiheuttama kiihtyvyys maan pinnalla on aina vakio: g = 9,8 m/s2
- Esimerkki: paino = m * g = 4, 2 * 9, 8 = 41, 16

Vaihe 4. Kirjoita vastauksesi muistiin
Edellinen vaihe ratkaisee ongelman ja antaa sinulle vastauksen.
Esimerkki: Normaalivoima on 41, 16 N
Menetelmä 2/5: Normaali voima kaltevalla tasolla
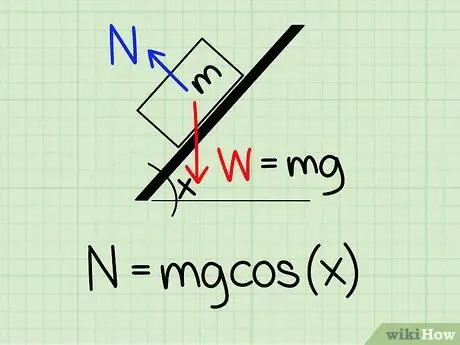
Vaihe 1. Käytä oikeaa yhtälöä
Jos haluat laskea normaalivoiman tiettyyn kulmaan kallistetulle esineelle, sinun on käytettävä kaavaa: N = m * g * cos (x)
- Tätä yhtälöä varten N symboloi normaalia tyyliä, m edustaa kohteen massaa g edustaa painovoiman aiheuttamaa kiihtyvyyttä, ja x edustaa vinoa kulmaa.
- Esimerkki: Etsi 4,2 kg: n kappaleen normaalivoima, joka lepää kaltevalla tasolla, jonka kaltevuus on 45 astetta.

Vaihe 2. Etsi kulman kosini
Kulman kosini on yhtä suuri kuin täydentävän kulman sini tai viereinen sivu jaettuna kaltevuuden muodostaman kolmion hypotenuusalla.
- Tämä arvo määritetään usein laskimella, koska minkä tahansa kulman kosini on aina vakio, mutta voit myös laskea sen manuaalisesti.
- Esimerkki: cos (45) = 0,71
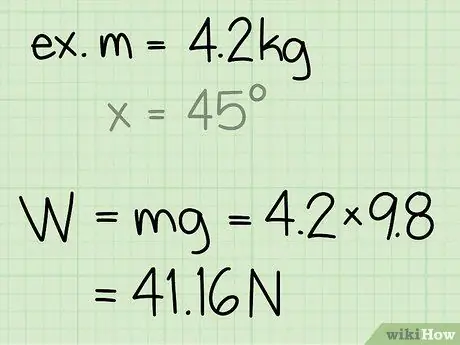
Vaihe 3. Etsi kohteen paino
Esineen paino on yhtä suuri kuin kohteen massa kertaa painovoimasta johtuva kiihtyvyys.
- Huomaa, että painovoiman aiheuttama kiihtyvyys maan pinnalla on aina vakio: g = 9,8 m/s2
- Esimerkki: paino = m * g = 4, 2 * 9, 8 = 41, 16
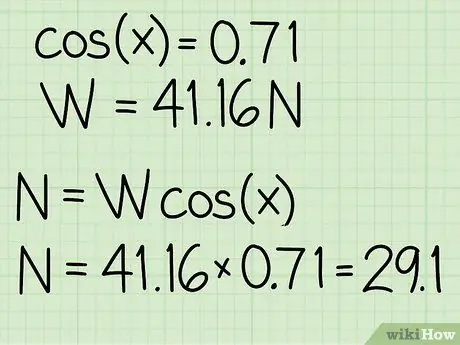
Vaihe 4. Kerro kaksi arvoa
Normaalivoiman löytämiseksi sinun on kerrottava kohteen paino kaltevuuskulman kosinilla.
Esimerkki: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
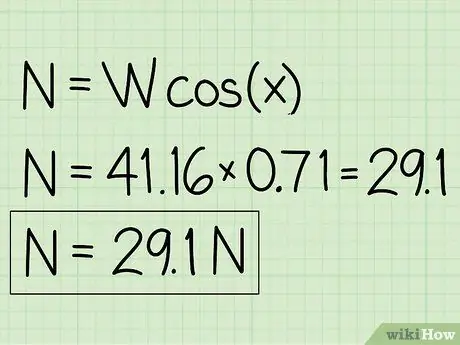
Vaihe 5. Kirjoita vastauksesi muistiin
Edellinen vaihe ratkaisee ongelman ja antaa vastauksesi.
- Huomaa, että kun esine on levossa rinteessä, normaalivoima on pienempi kuin esineen paino.
- Esimerkki: Normaalivoima on 29,1 N.
Tapa 3/5: Normaali tyyli ja ulompi alas -tyyli
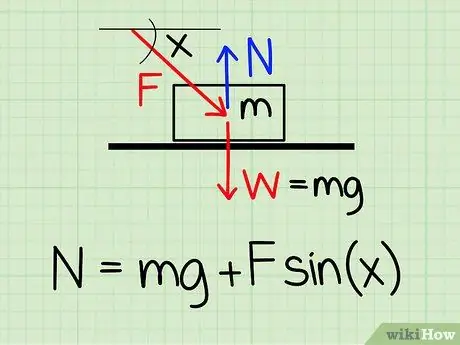
Vaihe 1. Käytä oikeaa yhtälöä
Jos haluat laskea normaalivoiman levossa olevaan kohteeseen, jos siihen kohdistuu ulkoinen alaspäin suuntautuva voima, käytä yhtälöä: N = m * g + F * sin (x) '
- N symboloi normaalia tyyliä, m edustaa kohteen massaa g kuvaa painovoiman aiheuttamaa kiihtyvyyttä, F symboloi ulkoista tyyliä ja x edustaa kohteen ja ulkoisen voiman suunnan välistä kulmaa.
- Esimerkki: Etsi 4,2 kg: n kappaleen normaalivoima, jos henkilö työntää esinettä 30 asteen kulmassa ja 20,9 N.
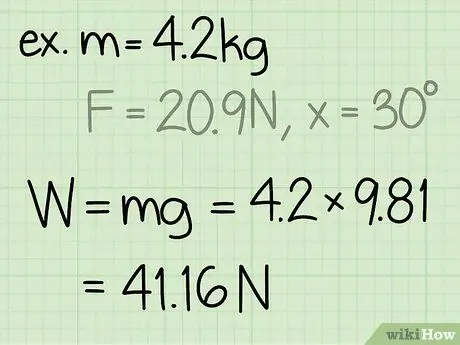
Vaihe 2. Etsi kohteen paino
Esineen paino on yhtä suuri kuin kohteen massa kertaa painovoimasta johtuva kiihtyvyys.
- Huomaa, että painovoiman aiheuttama kiihtyvyys maan pinnalla on aina vakio: g = 9,8 m/s2
- Esimerkki: paino = m * g = 4, 2 * 9, 8 = 41, 16
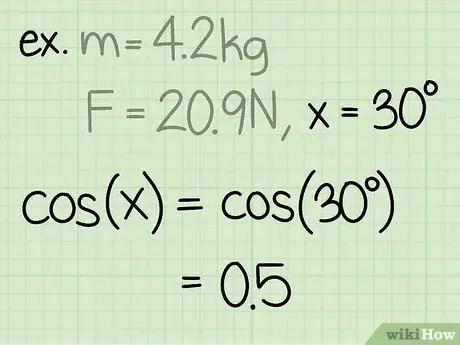
Vaihe 3. Etsi kulman sini
Kulman sini lasketaan jakamalla kulmaa vastakkainen kolmion sivu kulman hypotenuusalla.
Esimerkki: sin (30) = 0,5

Vaihe 4. Kerro sini ulkoisella voimalla
Ulkoinen voima tässä esimerkissä viittaa kohteeseen kohdistuvaan alaspäin suuntautuvaan voimaan.
Esimerkki: 0, 5 * 20, 9 = 10, 45
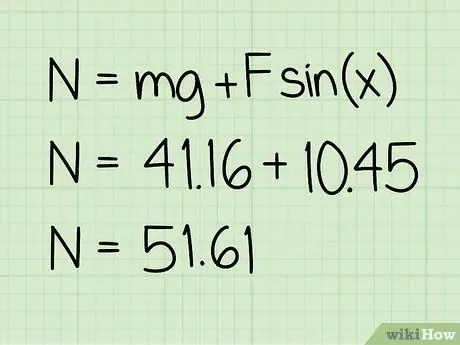
Vaihe 5. Lisää tämä arvo painoon
Tämä summa antaa normaalivoiman suuruuden.
Esimerkki: 10, 45 + 41, 16 = 51, 61
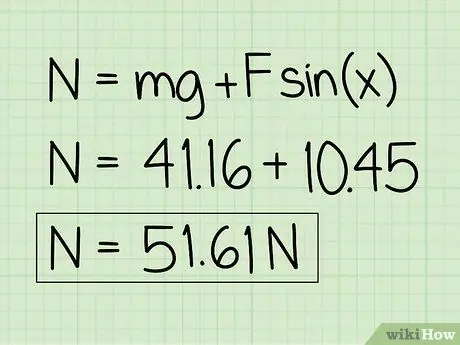
Vaihe 6. Kirjoita vastauksesi muistiin
Huomaa, että lepotilassa olevan esineen, johon ulkoinen alaspäin suuntautuva voima vaikuttaa, normaalivoima on suurempi kuin kohteen paino.
Esimerkki: Normaalivoima on 51,61 N
Menetelmä 4/5: Normaali tyyli ja ulkoinen tyyli ylös
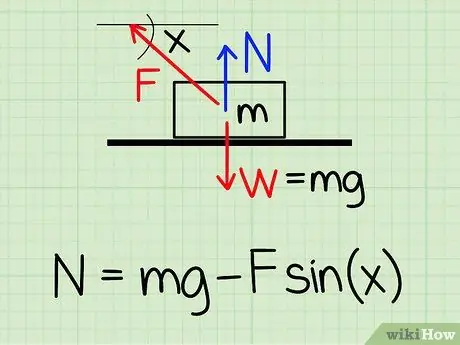
Vaihe 1. Käytä oikeaa yhtälöä
Jos haluat laskea normaalivoiman levossa olevaan kohteeseen, jos siihen kohdistuu ulkoinen ylöspäin suuntautuva voima, käytä yhtälöä: N = m * g - F * sin (x) '
- N symboloi normaalia tyyliä, m edustaa kohteen massaa g kuvaa painovoiman aiheuttamaa kiihtyvyyttä, F symboloi ulkoista tyyliä ja x edustaa kohteen ja ulkoisen voiman suunnan välistä kulmaa.
- Esimerkki: Etsi 4,2 kg: n kappaleen normaalivoima, jos joku vetää lohkoa ylöspäin 50 asteen kulmassa ja voimalla 20,9 N.

Vaihe 2. Etsi kohteen paino
Esineen paino on yhtä suuri kuin kohteen massa kertaa painovoimasta johtuva kiihtyvyys.
- Huomaa, että painovoiman aiheuttama kiihtyvyys maan pinnalla on aina vakio: g = 9,8 m/s2
- Esimerkki: paino = m * g = 4, 2 * 9, 8 = 41, 16
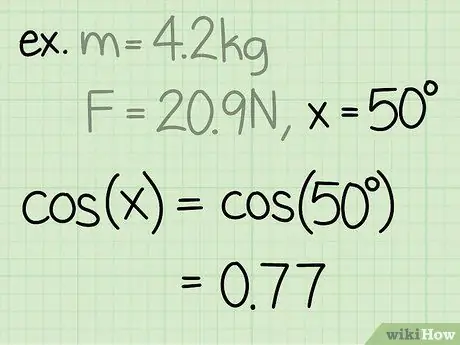
Vaihe 3. Etsi kulman sini
Kulman sini lasketaan jakamalla kulmaa vastakkainen kolmion sivu kulman hypotenuusalla.
Esimerkki: sin (50) = 0, 77

Vaihe 4. Kerro sini ulkoisella voimalla
Ulkoisella voimalla tarkoitetaan tässä tapauksessa ylöspäin suuntautuvaa voimaa, joka osuu esineeseen.
Esimerkki: 0,77 * 20, 9 = 16, 01
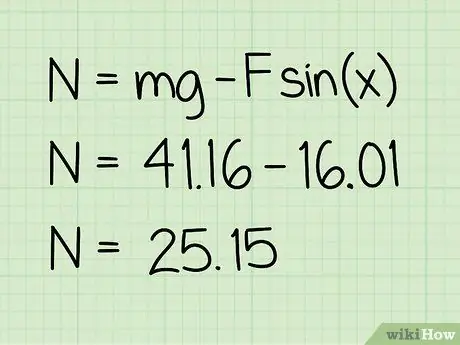
Vaihe 5. Vähennä tämä arvo painosta
Vähennys, jonka teet, antaa sinulle siihen vaikuttavan normaalivoiman suuruuden.
Esimerkki: 41, 16-16, 01 = 25, 15
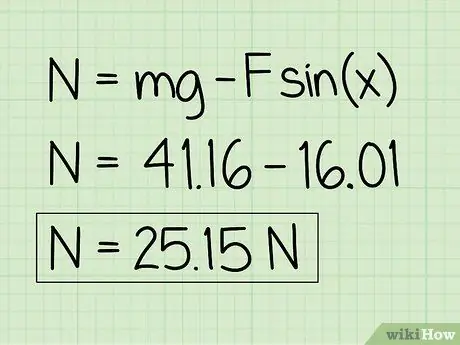
Vaihe 6. Kirjoita vastauksesi muistiin
Huomaa, että ylöspäin suuntautuva ulkoinen voima vaikuttaa lepotilassa olevaan esineeseen, normaalivoima on pienempi kuin kohteen paino.
Esimerkki: Normaalivoima on 25, 15 N
Menetelmä 5/5: Normaali voima ja kitka

Vaihe 1. Tiedä kineettisen kitkan perusyhtälö
Kineettinen kitka tai liikkuvan kohteen kitka on yhtä suuri kuin kitkakerroin kertaa kohteen normaali voima. Yhtälömuodossa: f = * N
- Tässä yhtälössä f symboloivat kitkaa, ️ edustaa kitkakerrointa, ja N edustaa kohteen normaalia voimaa.
- "Kitkakerroin" on kitkavoiman suhde normaalivoimaan, joka puristaa kaksi vastakkaista pintaa.
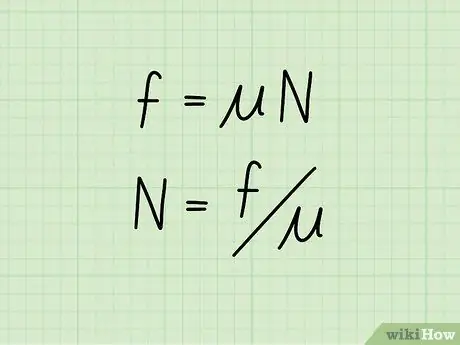
Vaihe 2. Määritä yhtälö normaalivoiman eristämiseksi
Jos tiedät kohteen kineettisen kitkan arvon ja sen kitkakertoimen, voit laskea normaalivoiman käyttämällä kaavaa: N = f /
- Alkuperäisen yhtälön molemmat puolet on jaettu ️, eristäen siten normaalivoiman toiselta puolelta samalla kun lasketaan kitka- ja kineettinen kitkakerroin toiselta puolelta.
- Esimerkki: Etsi lohkon normaalivoima, jos kitkakerroin on 0,4 ja kineettisen kitkan suuruus on 40 N.
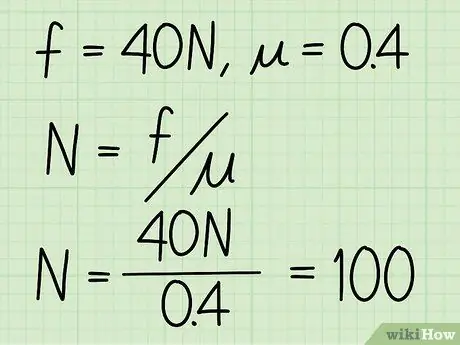
Vaihe 3. Jaa kineettinen kitka kitkakertoimella
Pohjimmiltaan tämä on kaikki mitä sinun tarvitsee tehdä löytääksesi normaalivoiman suuruuden.
Esimerkki: N = f / = 40 /0, 4 = 100
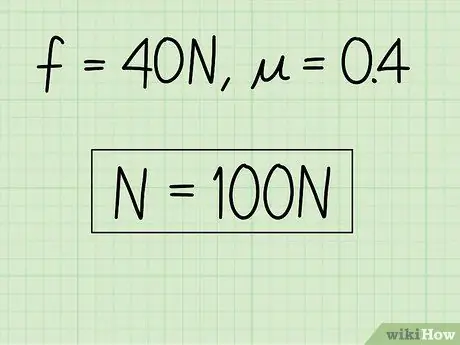
Vaihe 4. Kirjoita vastauksesi muistiin
Halutessasi voit tarkistaa vastauksesi liittämällä sen takaisin alkuperäiseen kineettisen kitkan yhtälöön. Jos et halua sitä, olet ratkaissut ongelman.






