Spearmanin sijoituskorrelaatiokertoimen avulla voimme tunnistaa, onko kahdella muuttujalla monotoninen funktiosuhde (toisin sanoen, kun yksi luku kasvaa, myös toinen numero kasvaa tai päinvastoin). Spearmanin sijoituskorrelaatiokerroimen laskemiseksi sinun on järjestettävä ja vertailtava tietojoukkoja löytääksesi d2ja syötä sitten tiedot Spearmanin vakio- tai yksinkertaistettuun korrelaatiokerroinkaavaan. Voit myös laskea nämä kertoimet käyttämällä Excel -kaavoja tai R -komentoa.
Vaihe
Menetelmä 1/3: Manuaalinen tapa
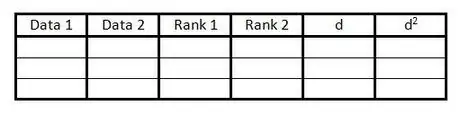
Vaihe 1. Luo taulukko
Taulukossa käytetään kaikkia tietoja, joita tarvitaan Spearman Rank -korrelaatiokerroimen laskemiseen. Tarvitset tällaisen taulukon:
- Luo kuusi saraketta otsikoilla, kuten esimerkissä.
- Valmista niin monta tyhjää riviä kuin tietopareja.
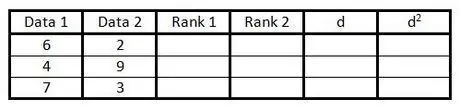
Vaihe 2. Täytä kaksi ensimmäistä saraketta datapareilla
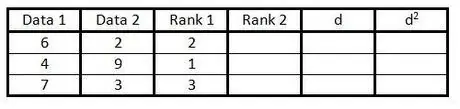
Vaihe 3. Anna kolmannen sarakkeen tietoryhmien ensimmäisen sarakkeen sijoitus 1: stä n: ään (tietojen määrä)
Anna arvosana 1 pienimmälle arvolle, 2 arvosana seuraavalle pienimmälle arvolle ja niin edelleen.
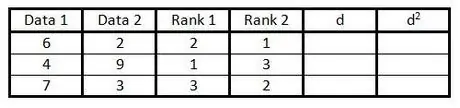
Vaihe 4. Toimi neljännessä sarakkeessa samalla tavalla kuin vaiheessa 3, mutta luokittele tiedot toisessa sarakkeessa
-
Keskiarvo_742 Jos kahdella (tai useammalla) arvolla on sama arvo, laske tietojen keskimääräinen luokitus ja syötä sitten taulukkoon tämän keskiarvon perusteella.
Oikealla olevassa esimerkissä luokituksissa 2 ja 3 on kaksi arvoa 5. 2: n ja 3: n keskiarvo on 2,5, joten anna arvosana 2,5 molemmille arvoille 5.
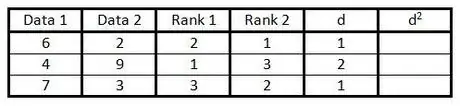
Vaihe 5. Laske sarakkeessa "d" erotus sijoitussarakkeen kahden numeron välillä
Toisin sanoen, jos yksi sarake on sijoittunut 1 ja toinen sarake luokkaan 3, ero on 2. (Merkillä ei ole väliä, koska seuraava vaihe on neliön arvo.)
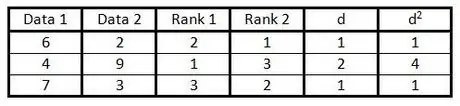
Vaihe 6. Neliöi jokainen numero sarakkeessa "d" ja kirjoita tulos sarakkeeseen "d2".
Vaihe 7. Lisää kaikki tiedot sarakkeeseen d2".
Tuloksena on d2.
Vaihe 8. Valitse yksi seuraavista kaavoista:
-
Jos mikään luokituksista ei ole sama kuin edellisessä vaiheessa, kirjoita tämä arvo yksinkertaistettuun Spearman Rank Correlation Coefficient -kaavaan
Vaihe 8_271 ja korvaa "n" dataparien lukumäärällä saadaksesi tuloksen.
Vaihe 9_402 -
Jos edellisessä vaiheessa on samanlainen sijoitus, käytä tavallista Spearman Rank Correlation Coefficient -kaavaa:
Spearman
Vaihe 9. Tulkitse tulokset
Arvo voi vaihdella välillä -1 ja 1.
- Jos arvo on lähellä -1, korrelaatio on negatiivinen.
- Jos arvo on lähellä 0, lineaarista korrelaatiota ei ole.
- Jos arvo on lähellä 1, korrelaatio on positiivinen.
Tapa 2/3: Excelin käyttäminen
Vaihe 1. Luo tiedoille uusi sarake ja niiden sijoitus
Jos tietosi ovat esimerkiksi sarakkeessa A2: A11, käytä kaavaa "= RANK (A2, A $ 2: A $ 11)" ja kopioi sitä alaspäin, kunnes se kattaa kaikki sarakkeet ja rivit.
Vaihe 2. Muuta samaa luokitusta menetelmän 1 vaiheissa 3 ja 4 kuvatulla tavalla
Vaihe 3. Laske uudessa solussa korrelaatio kahden sijoitussarakkeen välillä kaavalla "= CORREL (C2: C11, D2: D11)"
Tässä esimerkissä C ja D viittaavat sarakkeeseen, jossa sijoitus sijaitsee. Uusi solu täytetään Spearman Rank Correlationilla.
Tapa 3/3: R: n käyttö
Vaihe 1. Asenna ensin R -ohjelma, jos sinulla ei vielä ole sitä
(Katso
Vaihe 2. Tallenna tiedot CSV -muodossa, laita korrelaation etsimät tiedot kahteen ensimmäiseen sarakkeeseen
Voimme tehdä tämän käyttämällä Tallenna nimellä -valikkoa.
Vaihe 3. Avaa R Editor
Jos työskentelet päätelaitteesta, suorita vain R. Jos käytät työpöytää, napsauta R -kuvaketta.
Vaihe 4. Kirjoita seuraava komento:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") ja paina Enter.
- valettu (sijoitus (d [, 1]), sijoitus (d [, 2]))
Vinkkejä
Tietojen on koostuttava vähintään viidestä parista, jotta trendi voidaan nähdä (tietojen lukumäärä on esimerkissä 3 paria vain laskelmien yksinkertaistamiseksi.)
Varoitus
- Spearmanin sijoituskorrelaatiokerroin tunnistaa vain korrelaation voimakkuuden silloin, kun tiedot nousevat tai laskevat jatkuvasti. Jos tiedoissa on toinen suuntaus, Spearmanin sijoituskorrelaatio ei antaa tarkan esityksen.
- Tämä kaava perustuu oletukseen, että samanlaisia luokituksia ei ole. Kun on sama sijoitus kuin esimerkissä, meidän on käytettävä tätä määritelmää: kertoajan momentin korrelaatiokerroin.
