- Kirjoittaja Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:26.
- Viimeksi muokattu 2025-01-23 12:17.
Nopeus on lasku siitä, kuinka nopeasti jokin liikkuu kerrallaan. Jos olet koskaan katsonut liikkuvan auton nopeusmittaria, näet nopeuslaskennan - mitä kauemmas neula kulkee, sitä suurempi on ajoneuvon nopeus. Nopeuden laskemiseen on useita tapoja riippuen käytettävissä olevista tiedoista. Yleensä kaava nopeus = matka/aika (tai k = j/w) on helpoin tapa laskea nopeus.
Vaihe
Menetelmä 1/3: Vakionopeuslaskentakaavojen käyttäminen

Vaihe 1. Etsi kohteen matka
Peruskaava, jota useimmat ihmiset käyttävät löytääkseen nopeuden, on erittäin helppokäyttöinen. Ensinnäkin sinun on tiedettävä "kuinka paljon etäisyyttä mitattu objekti on kulkenut". Toisin sanoen, mikä on etäisyys kohteen lähtöpisteen ja päätepisteen välillä?
Tämä kaava on helpompi ymmärtää esimerkin avulla. Oletetaan, että matkustamme autolla leikkipaikalle "161 kilometriä". Muutamassa vaiheessa voimme käyttää näitä tietoja kaavan laskemisen loppuunsaattamiseen

Vaihe 2. Etsi aika, joka kestää kohteen kulkemaan kyseisen matkan
Seuraavaksi tarvitsemasi tieto on, kuinka kauan esine kestää saavuttaa tietyn etäisyyden. Toisin sanoen, kuinka kauan kestää, ennen kuin kohde siirtyy aloituspisteestä päätepisteeseen?
Tässä esimerkissä sanotaan, että objekti kestää n. kaksi tuntia päästäkseen määränpäähän.

Vaihe 3. Jaa etäisyys nopeudella, joka kuluu kohteen nopeuden löytämiseen
Tarvitset vain nämä kaksi tietoa tietääksesi kohteen nopeuden. Etäisyys aikaan on yhtä suuri kuin kohteen nopeus.
Tässä esimerkissä 161 kilometriä/2 tuntia = 80,5 kilometriä tunnissa.

Vaihe 4. Älä unohda käytettyä laitetta
On erittäin tärkeää käyttää oikeita yksiköitä vastauksessa (kuten kilometrejä tunnissa jne.) Ilman näitä yksiköitä ihmisten on erittäin vaikea ymmärtää vastauksesi merkitystä. Voit myös menettää pisteitä, jos käytät väärää yksikköä tehdessäsi koulutehtäviä.
Nopeuden yksikkö on etäisyysyksikkö ajan yksikköön. Esimerkiksi, koska mittaamme etäisyyden kilometreinä ja ajan tunteina, käytetyt yksiköt ovat kilometriä/tunti (tai kilometriä tunnissa).
Tapa 2/3: Vaikeampien laskelmien ratkaiseminen

Vaihe 1. Etsi useita erilaisia muuttujia etäisyyden ja ajan ongelman ratkaisemiseksi
Kun olet ymmärtänyt nopeuden peruskaavan, voit käyttää sitä muiden laskelmien suorittamiseen kuin nopeus. Jos esimerkiksi tiedät aluksi vain objektin nopeuden ja yhden muun muuttujan, voit järjestää yllä olevan kaavan uudelleen löytääksesi tuntemattomat tiedot.
-
Oletetaan esimerkiksi, että tiedämme, että juna kulkee 20 kilometriä tunnissa neljä tuntia, mutta emme tiedä kuinka pitkälle se on kulkenut. Selvittääksemme voimme järjestää kaavan uudelleen seuraavasti:
-
- nopeus = matka/aika
- nopeus × aika = (matka/aika) × aika
- nopeus × aika = etäisyys
- 20 km/tunti × 4 tuntia = etäisyys = 80 kilometriä
-

Vaihe 2. Muunna käyttämäsi yksiköt tarpeen mukaan
Joskus voit laskea nopeuden käyttämällä tiettyä yksikköä, mutta se on muunnettava toiseen yksikköön. Tässä tapauksessa sinun on käytettävä muuntokerrointa saadaksesi vastauksen oikeiden yksiköiden mukaan. Voit tehdä tämän kirjoittamalla yksiköiden välisen suhteen murtoluvussa ja kertomalla. Kun kerrot, käännä murto tarpeen mukaan poistaaksesi ei -toivotut yksiköt. Tämä menetelmä on paljon helpompi kuin miltä se kuulostaa!
-
Oletetaan esimerkiksi, että yllä olevassa esimerkkitehtävässä tarvitsemme vastauksen kilometreinä eikä mailina. Yksi kilometri vastaa noin 1,6 kilometriä. Joten voimme tehdä muunnoksen seuraavasti:
-
- 80 kilometriä × 1,6 kilometriä = 50 mailia
-
- Muista, että koska kilometrit näkyvät murto -osan alaosassa, se poistaa kilometrit edellisestä vastauksesta, joten lopputulos käyttää mailia.
- Tämä sivusto tarjoaa muunnosominaisuuksia useimmille yleisesti käytetyille yksiköille.

Vaihe 3. Korvaa "distance" -muuttuja etäisyyskaavalla tarpeen mukaan
Objektit eivät aina liiku suoralla, sileällä reitillä. Jos tämä on totta, et ehkä voi yksinkertaisesti syöttää numeerista arvoa etäisyysyksikkönä vakionopeuskaavaan. Saatat kuitenkin joutua korvaamaan kaavan k = j/w kirjaimen j kaavalla, joka muistuttaa kohteen kulkemaa matkaa.
-
Oletetaan esimerkiksi, että lentokone pyörii ilman läpi 20 mailin etäisyydellä 5 kertaa. Lentokone suoritti kierroksen puolessa tunnissa. Tässä esimerkissä meidän on vielä löydettävä lentokoneen kokonaismatka ennen kuin voimme määrittää sen nopeuden. Voimme käyttää kaavaa laskettaessa ympyrän etäisyys (etäisyys sen ympäriltä) j: n sijaan tässä kaavassa. Tämä kaava on ympärysmitta = 2πr jossa r = ympyrän säde. Voit ratkaista sen seuraavasti:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 mailia/tunti
-

Vaihe 4. Ymmärrä, että k = j/w antaa keskimääräisen nopeuden
Helppo ja yksinkertainen kaava, jota käytämme nopeuden löytämiseen, on yksi haittapuoli. Tuloksena oleva arvo on teknisesti keskimääräinen nopeus. Tämä tarkoittaa, että kaava olettaa, että mittaamasi kohde käyttää samaa nopeutta kuin se liikkuu. Kuten alla näemme, kohteen nopeuden löytäminen yhdessä hetkessä on paljon vaikeampaa.
Tämän eron havainnollistamiseksi kuvittele, milloin viimeksi matkustit autolla. On epätodennäköistä, että matkustat samalla nopeudella kuin matkustat. Yleensä kuitenkin aloitat matkan pienellä nopeudella ja lisäät nopeuttasi vähitellen matkan varrella pysähtyen punaisten valojen, liikenneruuhkien jne. Vuoksi. Jos käytät vakionopeuskaavaa nopeuden etsimiseen ajon aikana, nopeuden muutoksia ei voida havaita. Saat kuitenkin vastauksen, joka näyttää kaikkien matkustamiesi nopeuserojen keskimääräisen nopeuden
Tapa 3/3: Hetkellisen nopeuden laskeminen
Huomautus:
Tässä osassa käytetään tekniikoita, jotka ovat vähemmän tuttuja ihmisille, jotka eivät ole koskaan opiskelleet hammaskiveä. Lue apua laskelmia koskevista artikkeleistamme.
Vaihe 1. Ymmärrä, että nopeus määritellään kiihtyvyysnopeudeksi
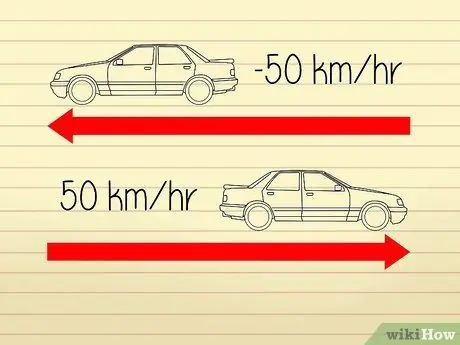
Korkean tason nopeuslaskelmat ovat melko hämmentäviä, koska matemaatikot ja tiedemiehet käyttävät erilaisia määritelmiä kuvaamaan "nopeutta" ja "kiihtyvyyttä". Kiihtyvyydessä on kaksi osaa: "nopeus" ja "suunta". Nopeus on sama kuin kohteen nopeus. Suunnan muutos muuttaa kiihtyvyyttä, mutta ei nopeutta.
- Oletetaan esimerkiksi, että kaksi autoa liikkuu vastakkaisiin suuntiin. Molempien autojen nopeusmittarit näyttävät 50 km/h, joten molemmat kulkevat samalla nopeudella. Koska autot ovat kuitenkin siirtymässä toisistaan, voimme sanoa, että toisen auton kiihtyvyys on -50 km/h, kun taas toisen kiihtyvyys on 50 km/h.
- Aivan kuten hetkellisiä nopeuslaskelmia, voit myös suorittaa hetkellisiä kiihtyvyyslaskelmia.

Vaihe 2. Käytä absoluuttisia arvoja negatiivisen kiihtyvyyden mittaamiseen
Kohteella voi olla negatiivinen kiihtyvyys (jos se liikkuu negatiiviseen suuntaan suhteessa toiseen kohteeseen). Negatiivista nopeutta ei kuitenkaan ole. Joten tässä tapauksessa nopeuden absoluuttinen arvo osoittaa kohteen nopeuden.
Tästä syystä yllä olevassa esimerkkiongelmassa molempien autojen nopeus on 50 km/h.
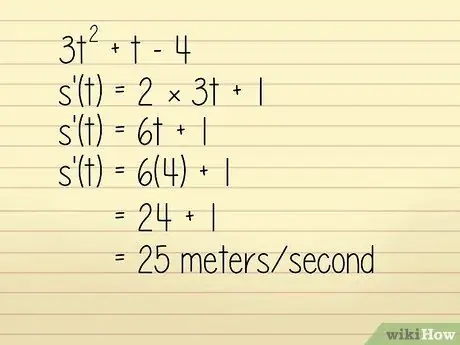
Vaihe 3. Ota funktion sijainnin derivaatta
Jos sinulla on funktio k (w), joka näyttää objektin sijainnin ilman, että aikaa tarvitsee laskea, k (w) -johdannainen näyttää kiihtyvyyden ilman ajoitusta. Liitä aika -arvo tähän kaavaan niin, että muuttuja w (tai mitä tahansa aika -arvoa käytetään) kiihtyy kyseisen ajan mukaan. Täältä löydät helposti kohteen nopeuden.
-
Oletetaan esimerkiksi, että kohteen sijainti metrissä kuvataan yhtälössä 3q2 + w - 4 jossa w = aika sekunneissa. Haluamme tietää objektin nopeuden w = 4 sekuntia. Tässä tapauksessa voit ratkaista sen seuraavasti:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Nyt kirjoitetaan w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 metriä sekunnissa. Teknisesti tämä on kiihtyvyyslaskelma, mutta koska se on positiivinen eikä suuntaa ole mainittu kysymyksessä, voimme käyttää sitä nopeuden löytämiseen.
-

Vaihe 4. Ota integroitu kiihdytystoiminto
Kiihtyvyys on tapa mitata objektin kiihtyvyyden muutos ajan mittaan. Tämä aihe on liian monimutkainen selitettäväksi tässä artikkelissa. On kuitenkin hyödyllistä huomata, että kun sinulla on funktio a (w), joka edustaa kiihtyvyyttä ajan suhteen, a (w) -integraali palauttaa kiihtyvyyden tuloksen kyseisen ajan perusteella. Muista, että on erittäin hyödyllistä tietää objektin alkukiihtyvyys, jotta voit määrittää tuloksen vakion äärettömästä integraalista.
-
Oletetaan esimerkiksi, että objektilla on jatkuva kiihtyvyys (m/s2 seurauksena (w) = -30. Sano myös, että kohteen kiihtyvyys on 10 m/s. Meidän on löydettävä nopeus w = 12 sekuntia. Tässä tapauksessa voimme ratkaista sen seuraavasti:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C.
-
-
C: n löytämiseksi ratkaisemme p (w), kun w = 0. Muista, että kohteen alkuperäinen kiihtyvyys on 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, joten p (w) = -30w + 10
-
-
Nyt voimme kirjoittaa w = 12 sekuntia.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Koska nopeus on kiihtyvyyden absoluuttinen arvo, kohteen nopeus on 350 metriä/sekunti.
-
Vinkkejä
- Harjoittelu tekee hienoa! Yritä luoda oma kysymyksesi korvaamalla yllä olevan esimerkkitehtävän numerot.
- Jos etsit nopeaa tapaa harjoitella laskentaa paremman laskentanopeuden saavuttamiseksi, käytä online -johdannaislaskinta täällä ja online -integraalilaskinta täällä.






