- Kirjoittaja Jason Gerald [email protected].
- Public 2023-12-16 11:09.
- Viimeksi muokattu 2025-01-23 12:17.
Desimaalilukujärjestelmässä on kymmenen mahdollista arvoa (0, 1, 2, 3, 4, 5, 6, 7, 8 tai 9) kullekin numeroasemalle. Sitä vastoin binäärisessä (peruskanta) numerojärjestelmässä on vain kaksi mahdollista arvoa, joita edustavat 0 ja 1 kullekin numeroasemalle. Koska binäärilukujärjestelmä on elektronisten tietokoneiden sisäinen kieli, vakavat tietokoneohjelmoijat osaavat muuntaa desimaalijärjestelmän binäärilukujärjestelmäksi. Noudata näitä helppoja ohjeita ja myös kuinka voit hallita tämän muunnoksen.
Vaihe
Menetelmä 1/2: Lyhyt jakaminen kahdella jäljellä

Vaihe 1. Määritä ongelma
Tässä esimerkissä muunnetaan desimaaliluku 15610 olla binääriluku. Kirjoita desimaaliluku jaettavaksi numeroksi käänteisen jakosymbolin kohdalle. Kirjoita kohdenumerojärjestelmän perusta (tässä esimerkissä "2" binaarille) jakosymbolin kaarevaksi jakajaksi.
- Tämä menetelmä on paljon helpompi ymmärtää, kun se piirretään paperille, ja paljon helpompaa aloittelijoille, koska se jakaa vain kahdella.
- Välttääksesi sekaannukset ennen muuntamista ja sen jälkeen, kirjoita laskettavan numerojärjestelmän perusnumero alaindeksiksi (pienet kirjaimet tavallisilla kirjaimilla erotusmerkkinä) kullekin numerolle. Tässä esimerkissä desimaaliluvulla on alaindeksi 10 ja binääriluvulla alaindeksi 2.

Vaihe 2. Tee jako
Kirjoita kokonaisluvun vastaus (osamäärä) pitkän jakosymbolin alle ja loput (0 tai 1) jaetun numeron oikealle puolelle.
Koska jaamme kahdella, kun jaettava luku on parillinen luku, loppuosa on 0 ja kun jaettava luku on pariton luku, loput on 1

Vaihe 3. Jatka jakamista, kunnes se saavuttaa nollan
Jatka alamäkeä jakamalla jokainen uusi osamäärä kahdella ja kirjoittamalla loput kunkin jaetun numeron oikealle puolelle. Lopeta, kun osamäärä on nolla.

Vaihe 4. Kirjoita uusi binääriluku muistiin
Aloita pienimmästä jäljellä olevasta numerosta ja lue loput järjestyksestä nousevaan järjestykseen alkuun. Tässä esimerkissä sinun pitäisi saada tulos 10011100. Tämä on desimaaliluvun 156. binäärinen vastine. Tai jos se on kirjoitettu sen numeerisen perusindeksin kanssa: 15610 = 100111002.
Tätä menetelmää voidaan muuttaa muuntaa desimaalikannasta mihin tahansa numeropohjaan. Jakaja on 2, koska kohdenumerojärjestelmän perusta on kanta 2 (binääri). Jos kohdenumerojärjestelmän tukikohta on toinen tukiasema, korvaa tämän menetelmän perusnumero 2 sopivalla tukiluvulla. Jos kohdekanta on esimerkiksi tukikohta 9, korvaa tukiaseman 2 numero yhdeksällä. Lopputulos on suoraan kohdekannan muodossa
Menetelmä 2/2: Kahden johtaminen ja vähennyslasku

Vaihe 1. Aloita luomalla taulukko
Kirjoita kahden perusnumeron tehot "taulukon 2 pohjaan" oikealta vasemmalle. Aloita 20, kirjoita se "1". Nosta sijoitusta 1 jokaisella arvolla. Täytä taulukko, kunnes saat luvun, joka on lähimpänä laskemaasi desimaalilukujärjestelmää. Tässä esimerkissä muunnetaan desimaaliluku 15610 olla binääriluku.

Vaihe 2. Etsi numero, jolla on kantaluvun 2 suurin voima
Valitse taulukosta suurin luku, joka on yhtä suuri tai pienempi kuin muunnettava luku. Numero 128 on numero, jolla on kantaluvun 2 suurin voima ja joka on myös pienempi kuin 156, joten kirjoita numero "1" tämän taulukon alle, jossa taulukon suurin numero on vasemmalla (katso taulukko yllä olevassa kuvassa). Vähennä sitten 128 alkuperäisestä numerosta, saat: 156-128 = 28.
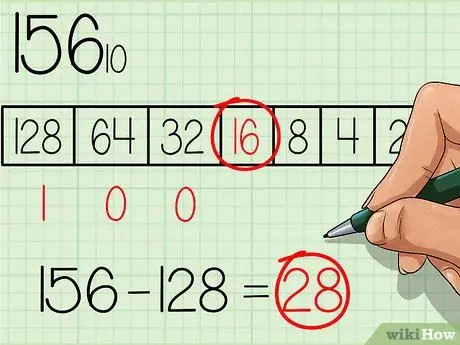
Vaihe 3. Siirry taulukon seuraavaan pienempään tehoon
Käytä uutta numeroa (28), jatka taulukon läpi vasemmalta oikealle ja tarkista, ovatko luvut yhtä suuria tai pienempiä kuin uusi numero. Numero 64 on vähintään 28, joten kirjoita numero”0” numerokenttään 64. Jatka, kunnes löydät luvun, joka on yhtä suuri tai pienempi kuin 28.
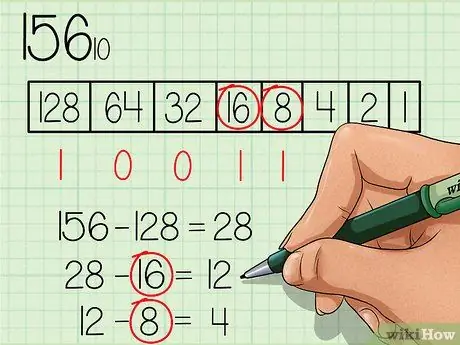
Vaihe 4. Vähennä jatkuvasti jokainen numero, joka on yhtä suuri tai pienempi kuin uusi numero, ja merkitse asianmukainen numero ruudun alapuolelle
Numero 16 on alle 28, joten kirjoita numero "1" numerokentän 16 alle ja vähennä 16 numerosta 28, jolloin saat uuden numeron 12. Numero 8 on alle 12, joten kirjoita numero "1" alle saat numeron 4 ja vähennät 8 numerosta 12.

Vaihe 5. Jatka, kunnes saavut taulukon loppuun
Muista merkitä "1" jokaisen ruudun alle, jos numero on sama tai pienempi kuin uusi numero, ja "0" jokaisen ruudun alle, jos numero on vielä suurempi kuin uusi numero.
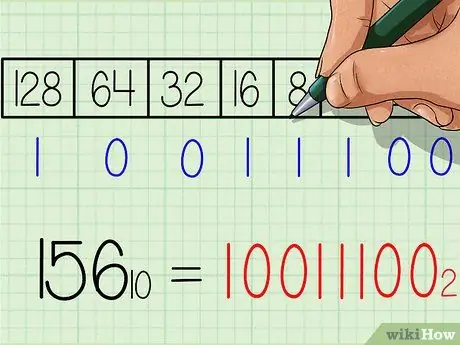
Vaihe 6. Kirjoita binääriluvun vastaus muistiin
Numero on täsmälleen sama vasemmalta oikealle kuin taulukon alareunassa olevat numerorivit "1" ja "0". Sinun pitäisi saada tulos 10011100. Tämä on desimaaliluvun 156. binäärinen vastine. Tai kun kirjoitetaan alaindeksillä: 15610 = 100111002.
Tämän menetelmän toistaminen voi auttaa sinua muistamaan kantaluvun kaksi tehot, joten voit ohittaa vaiheen 1
Vinkkejä
- Käyttöjärjestelmään rakennettu Laskin -ohjelma voi tehdä tämän muunnoksen puolestasi, mutta ohjelmoijana on parasta aloittaa ymmärtämällä hyvin, miten konversiot toimivat. Laskin -ohjelman muunnosvaihtoehdot voidaan tuoda näkyviin avaamalla Näytä -valikko ja valitsemalla Ohjelmoija (Windows 7 ja 8).
- Muuntaminen vastakkaiseen suuntaan eli binaariluvusta desimaalilukujärjestelmään on yleensä helpompi oppia ensin.
- Harjoittele usein desimaalilukujen muuntamista binaariksi, jotta sinusta tulee asiantuntija.






