Matriisi on suorakulmainen järjestely numeroista, symboleista tai lausekkeista riveillä ja sarakkeissa. Jos haluat kertoa matriisin, sinun on kerrottava matriisin ensimmäisen rivin elementit (tai numerot) matriisin toisen rivin elementeillä ja laskettava tuote yhteen. Voit kertoa matriiseja vain muutamalla helpolla vaiheella, jotka edellyttävät tulosten oikeaa lisäämistä, kertomista ja sijoittamista.
Vaihe
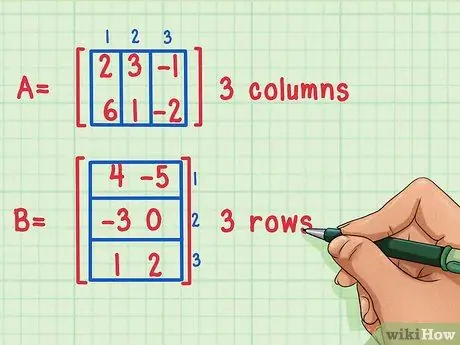
Vaihe 1. Varmista, että matriisit ovat kertoja
Voit kertoa matriisin vain, jos ensimmäisen matriisin sarakkeiden määrä on yhtä suuri kuin toisen matriisin rivien määrä.
Nämä matriisit voidaan kertoa, koska ensimmäisessä matriisissa, matriisissa A, on 3 saraketta, kun taas toisessa matriisissa, matriisissa B, on 3 riviä
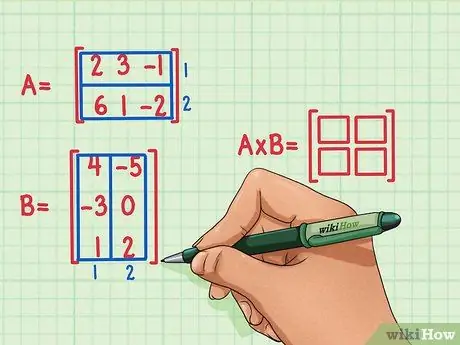
Vaihe 2. Merkitse matriisituotteen mitat
Luo uusi tyhjä matriisi, joka merkitsee kahden matriisin tulon mitat. Matriisissa, joka edustaa matriisin A ja matriisin B tulosta, on sama määrä rivejä kuin ensimmäisessä matriisissa ja sama määrä sarakkeita kuin toisessa matriisissa. Voit piirtää tyhjiä ruutuja näyttääksesi tämän matriisin rivien ja sarakkeiden määrän.
- Matriisissa A on 2 riviä, joten matriisin kertomisen tuloksena on 2 riviä.
- Matriisissa B on 2 saraketta, joten matriisin kertomisen tuloksena on 2 saraketta.
- Matriisituloksen tuloksena on 2 riviä ja 2 saraketta.
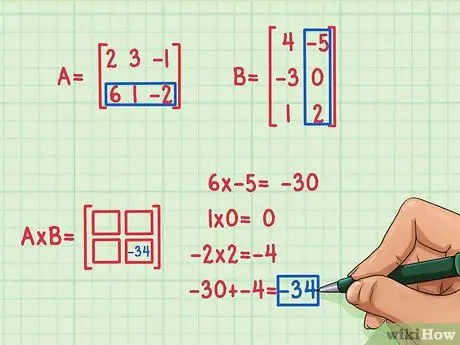
Vaihe 3. Etsi ensimmäisen pistetuloksen tulos
Jos haluat löytää ensimmäisen pistetuloksen tuloksen, sinun on kerrottava ensimmäisen rivin ensimmäinen elementti ensimmäisen sarakkeen ensimmäisellä elementillä, ensimmäisen rivin toinen elementti ensimmäisen sarakkeen toisella elementillä ja kolmas elementti ensimmäinen rivi ensimmäisen sarakkeen kolmannella elementillä. Lisää sitten kertolaskut yhteen löytääksesi piste tuote (piste).
Oletetaan, että olet päättänyt ensin laskea matriisituloksen toisen rivin ja toisen sarakkeen (oikeassa alakulmassa) elementit. Näin teet sen:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Pistetuloksen tulos on -34 ja tämä tulos kirjoitetaan matriisituloksen oikeaan alakulmaan.
Kun kerrot matriisin, pistetulo kirjoitetaan ensimmäisen matriisin rivikohtaan ja toisen matriisin sarakkeen sijaintiin. Esimerkiksi, kun tiedät matriisin A alarivin pistetuloksen ja matriisin B oikeanpuoleisen sarakkeen, vastaus -34 kirjoitetaan matriisituloksen alimmalle riville ja oikealle sarakkeelle
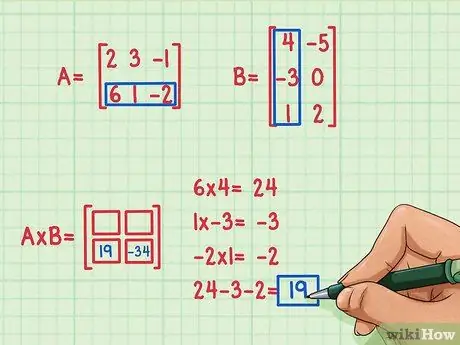
Vaihe 4. Etsi toisen pistetuloksen tulos
Oletetaan, että haluat löytää termin matriisituotteen vasemmasta alakulmasta. Tämän termin löytämiseksi sinun on vain kerrottava ensimmäisen matriisin alimman rivin elementit toisen matriisin ensimmäisen sarakkeen elementeillä ja lisättävä ne sitten yhteen. Käytä samaa menetelmää kuin kertomalla ensimmäinen rivi ja sarake - etsi uudelleen pisteellinen tuote (älä t)hänen.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Pistetuloksen tulos on -19 ja tämä tulos kirjoitetaan matriisituloksen vasempaan alakulmaan.
Vaihe 5. Etsi kaksi muuta pistetuotetta
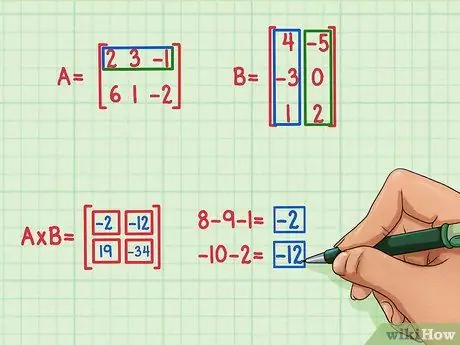
Jos haluat löytää termin matriisituotteen vasemmasta yläkulmasta, aloita etsimällä matriisin A ylärivin ja matriisin B vasemmanpuoleisen sarakkeen pistetulo. Näin teet sen:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Pistetuloksen tulos on -2 ja tämä tulos kirjoitetaan matriisituloksen vasempaan yläkulmaan.
Jos haluat löytää termin matriisituotteen oikeasta yläkulmasta, etsi vain matriisin A ylärivin pistematka ja matriisin B oikea sarake. Näin teet sen:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Pistetulo on -12 ja tämä tulos kirjoitetaan matriisituloksen oikeaan yläkulmaan.
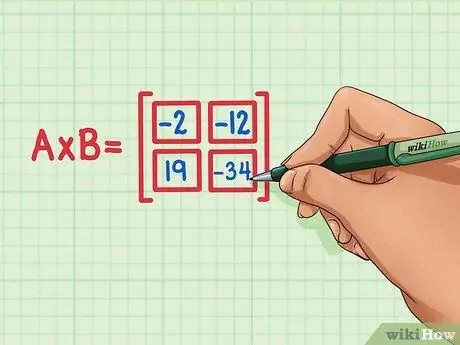
Vaihe 6. Varmista, että neljän pisteen tuotteet ovat oikeassa paikassa matriisituotteessa
19 on oltava vasemmassa alakulmassa, -34 on oltava oikeassa alakulmassa, -2 on oltava vasemmassa yläkulmassa ja -12 on oltava oikeassa yläkulmassa.
Vinkkejä
- Rivisegmenttien käyttäminen eikä viivojen käyttäminen voi antaa väärän vastauksen. Jos riviä edustava viiva vaatii jatkoa sarakkeen ylittämiseksi, pidennä sitä! Tämä on vain visualisointitekniikka, jonka avulla on helpompi tietää, mitä rivejä ja sarakkeita käytetään tuotteen kunkin elementin kanssa työskentelyyn.
- Kahden matriisin tulo tuottaa rivien määrän, joka on yhtä suuri kuin ensimmäisen matriisin rivien määrä ja sarakkeiden lukumäärä, joka vastaa toisen matriisin sarakkeiden määrää.
- Kirjoita summa ylös. Matriisien kertominen sisältää paljon laskelmia, ja on erittäin helppoa päästä sivuttain ja unohtaa, mikä luku kerrotaan.
